第三章对抗搜索

博弈问题

一人一步、信息完备、零和博弈.
通常不具有穷举性 (棋类问题).

极小-极大模型

目标: 对方不犯错的情况下结局对自己有利 (有利节点的数值>0).
圆形为极小节点, 正方形为极大节点, 自己应该始终沿着极大值行进.
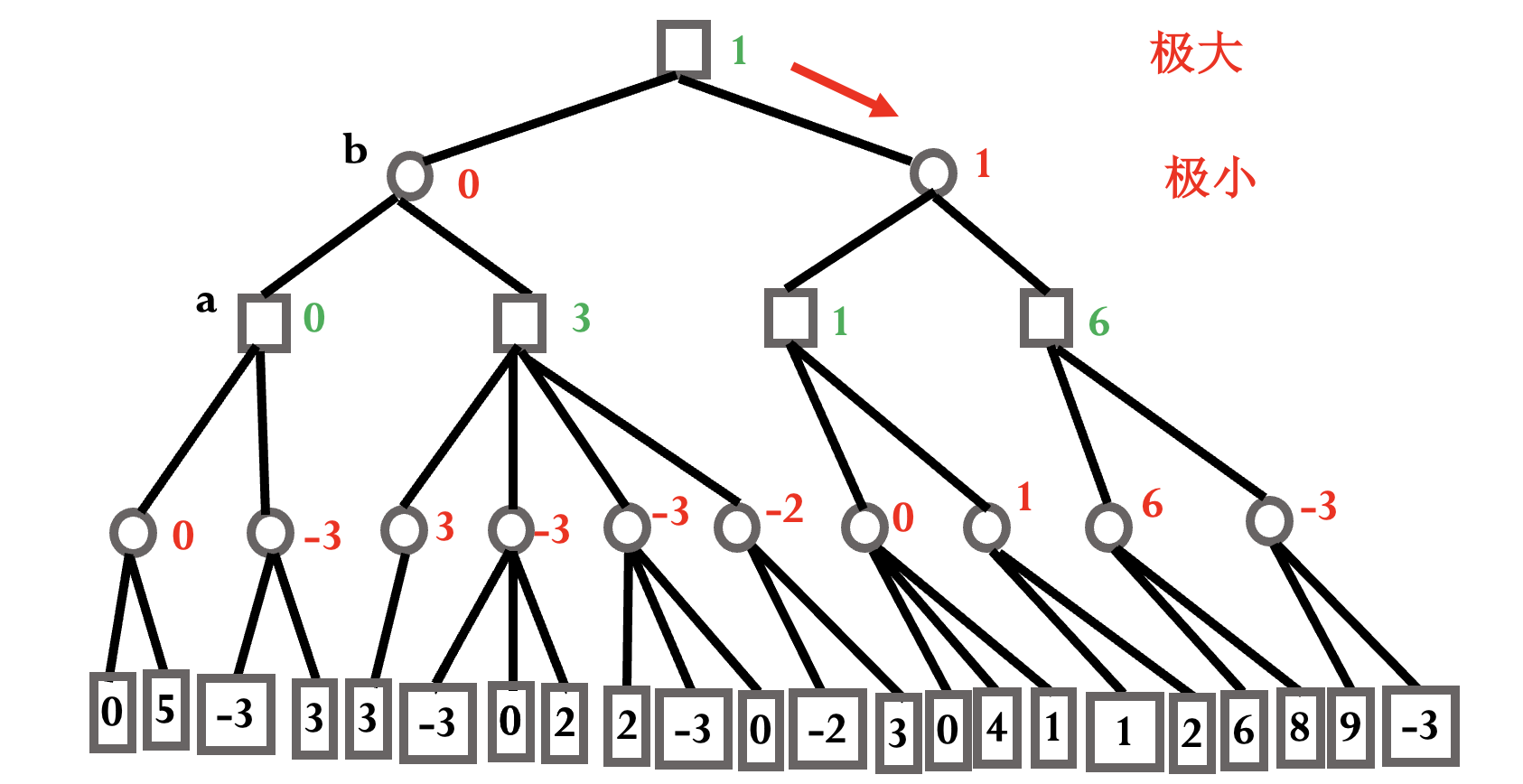
模仿人类下棋思考过程, 但有限深度内的穷举不可行.
为解决模型存在的问题, 只在少数可能的走步范围内考虑.

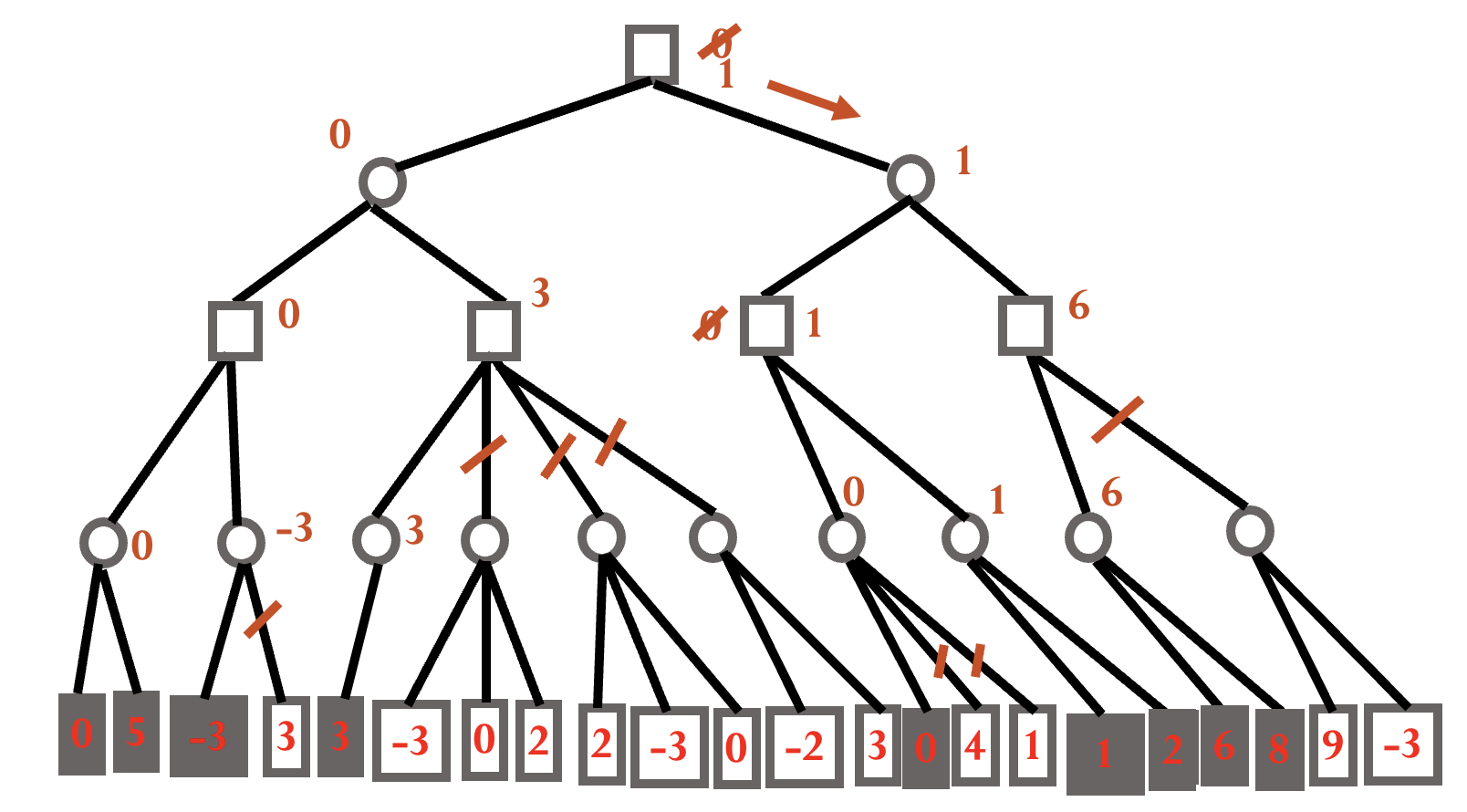
$\alpha$-$\beta$ 减枝算法

极大节点的下界为 $\alpha$, 极小节点的上界为 $\beta$, 使用 DFS 生成节点.
剪枝条件:
- 后辈节点的 $\beta$ 值 ≤ 祖先节点的 $\alpha$ 值时, $\alpha$ 剪枝.
- 后辈节点的 $\alpha$ 值 ≥ 祖先节点的 $\beta$ 值时, $\beta$ 剪枝.
简记:
- 极小 ≤ 极大, 剪枝.
- 极大 ≥ 极小, 剪枝.
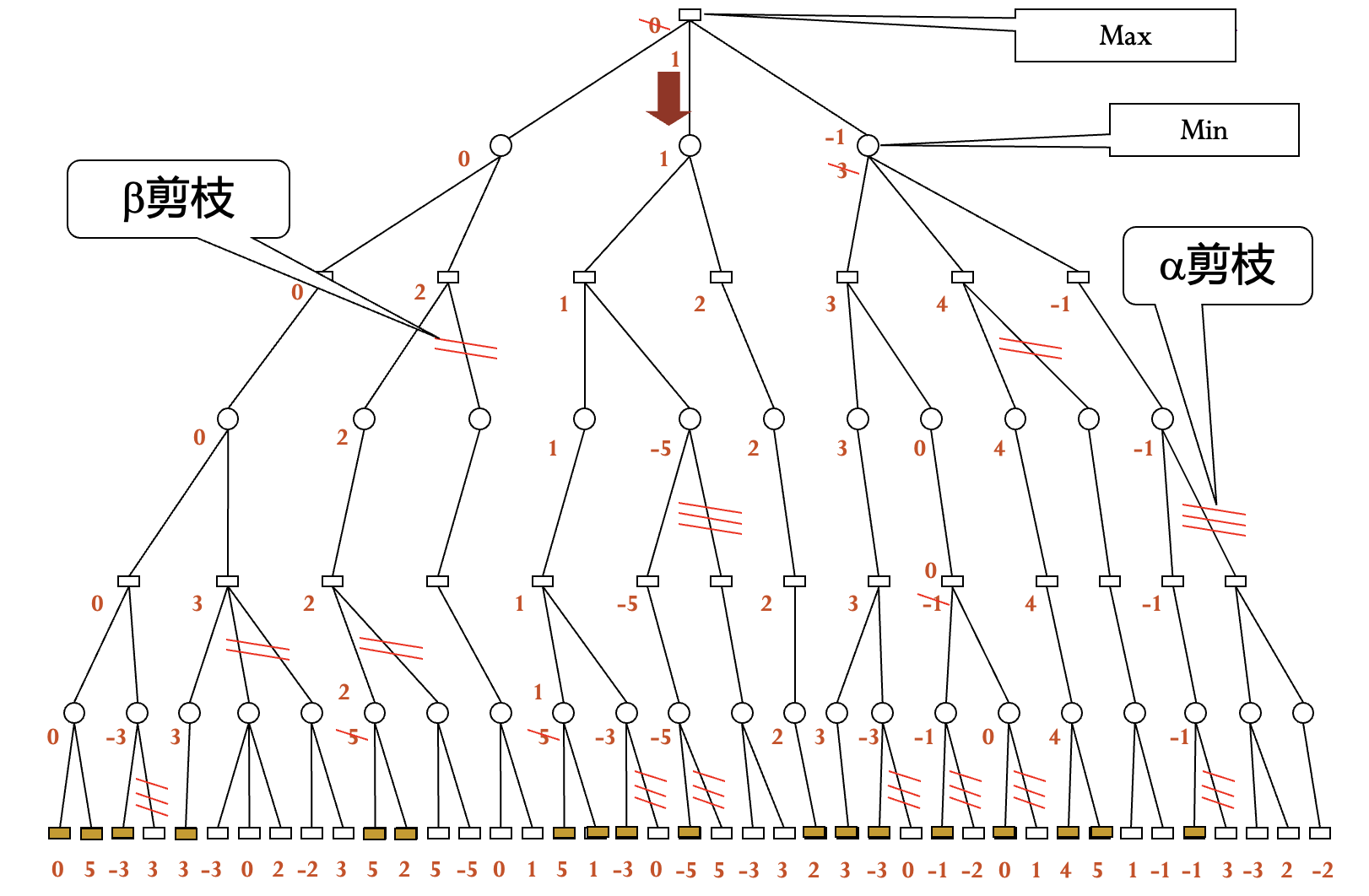
注意:
- 估值需要总结专家知识.
- 比较大小需要所有祖先节点进行比较.
- 先决定是否剪枝, 再决定是否上传.
- $\alpha$-$\beta$ 减枝仅能决定接下来一步的最优选择.
- 对局面评估的准确性要求高.

Monte Carlo 方法

从所有可落子点随机选择, 重复直到胜负可判断, 多次模拟选择胜率最大的点.
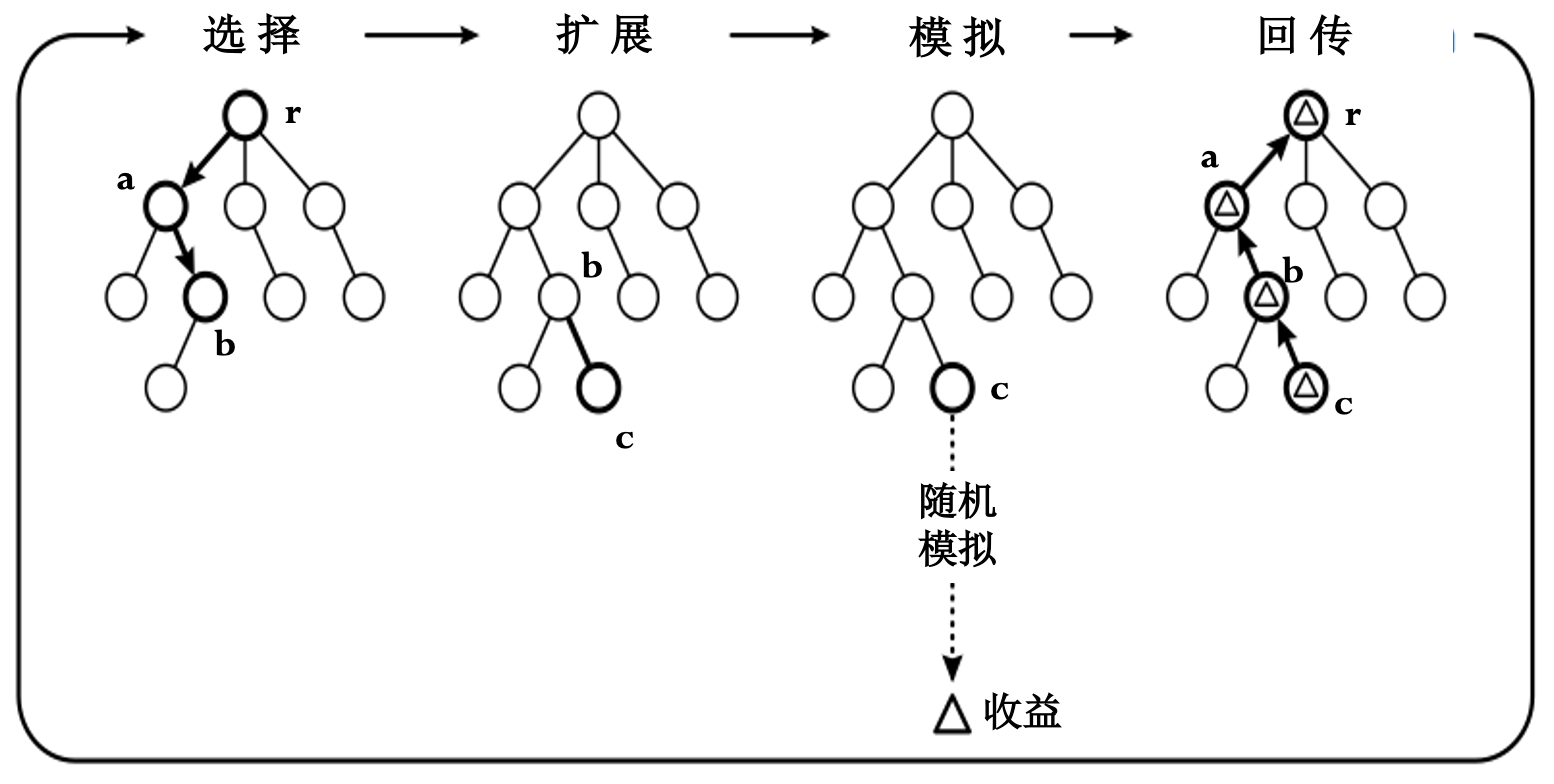
(MCTS) 蒙特卡洛树搜索:
- 将可能出现的状态转移过程用状态树表示.
- 从初始状态开始重复抽样, 逐步扩展.
- 树中的节点父节点可以利用子节点的模拟结果，提高了效率.
- 在搜索过程中可以随时得到行为的评价.
- 选择策略:
  - 对具有较大希望节点的利用.
  - 对尚未充分了解节点的探索.
(UCB) 信心上限算法:
```
def UCB1:
		for each j in 拉杆:
				访问 j 并记录收益
		while 尚未达到访问次数限制:
				计算每个拉杆的 UCB1 信心上界 Ij
				访问信心上界最大的拉杆
```
- $\overline{X}_j$ 是拉杆 $j$ 所获得回报的均值.
- $n$ 是到当前这一时刻为止所访问的总次数.
- $T_j(n)$ 是拉杆 $j$ 到目前为止所访问的次数.
- 上式考虑了 “利用” 和 “探索” 间的平衡.

(UCT) 信心上限树算法:

def UctSearch(s0):
  	'''
  	TREEPOLICY:
	  		节点还可扩展--扩展并模拟
				节点不可扩展--从子节点选择一个并循环
  	'''
		以状态s0创建根节点v0;
    while 尚未用完计算时长:
	      vl = TreePolicy(v0);
  	    △ = DefaultPolicy(s(vl));
    	  Backup(vl，△);
		return a(BestChild(v0，0));

每个节点记录: 获胜次数 / 模拟总次数.
获胜次数相对于本节点角度, 方便进行选择.
假设 $c=0$, 此时 $I_j=\overline{X}_j$.

AlphaGo 原理

MCTS 存在的问题:
- 生成所有子节点.
- 模拟具有盲目性.
AlphaGo 中神经网络与 MCTS 结合:
- 缩小了搜索范围.
- 提高了模拟水平.
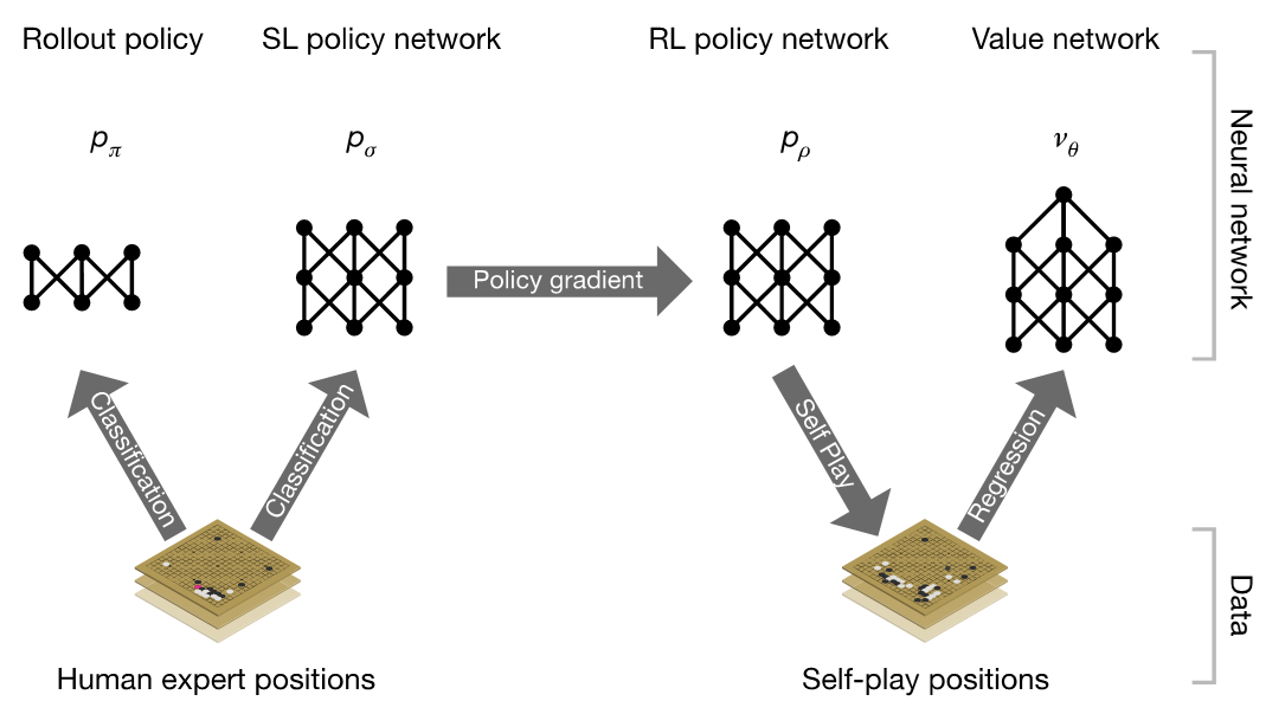
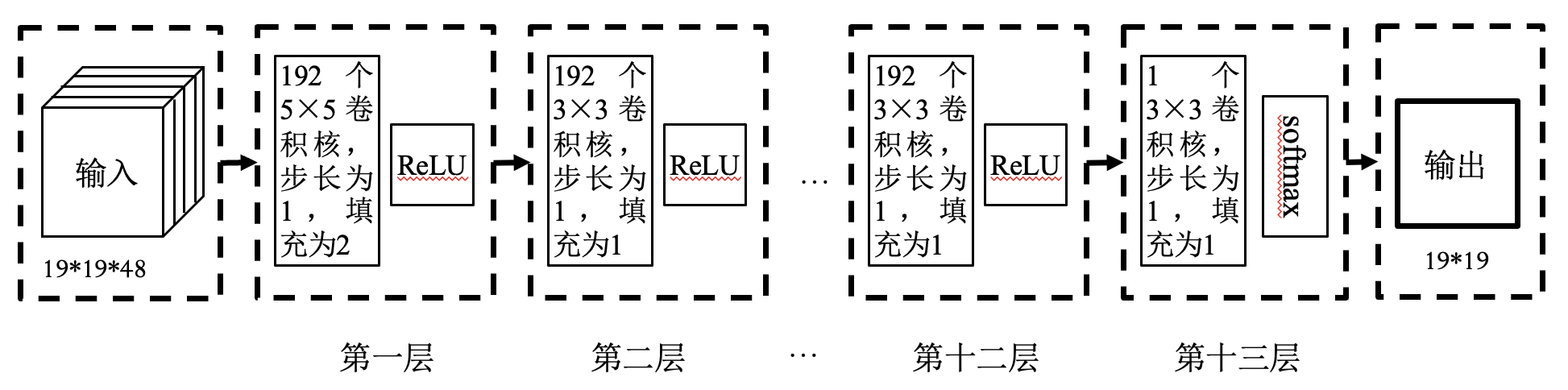
- 策略网络:
  - 输入: 当前棋局 —— 48 个通道, 每个通道大小为 19*19.
  - 输出: 棋盘上每个点的行棋概率 —— 概率越大, 行棋点越好.
  - 训练数据: 16 万盘人类棋手的数据.
  - 分类问题: 任意一个棋局分类为 361 类之一, 行棋点为标记.
  - 损失函数:
    $L(w)=-t_a\log p_a.$
    其中 $t_a$ 为当前棋局下棋手落子在 $a$ 处时为 1, 否则为 0; $p_a$ 为策略网络在 $a$ 处落子的概率.
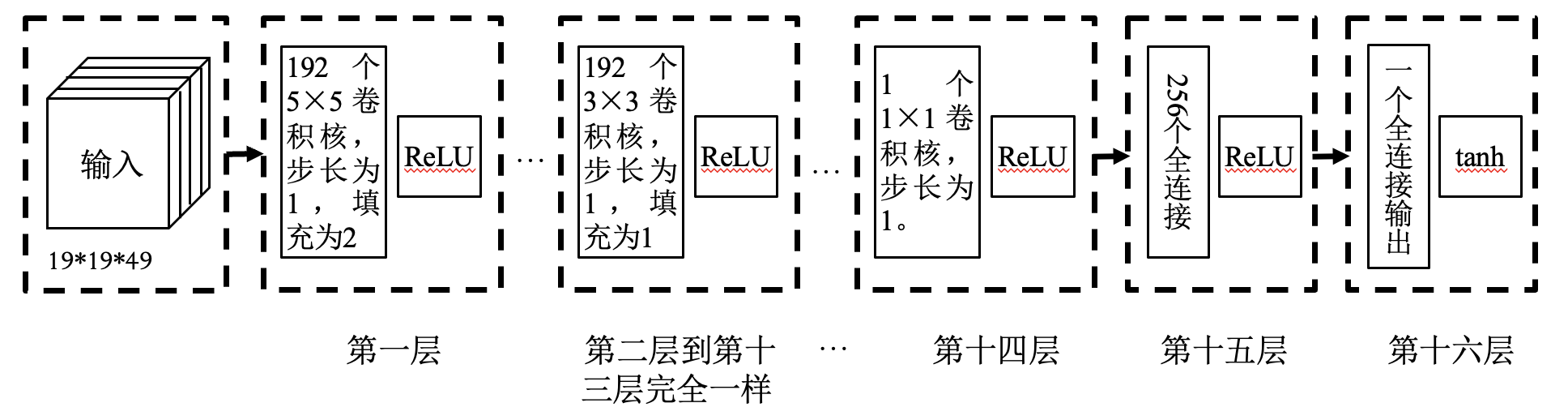
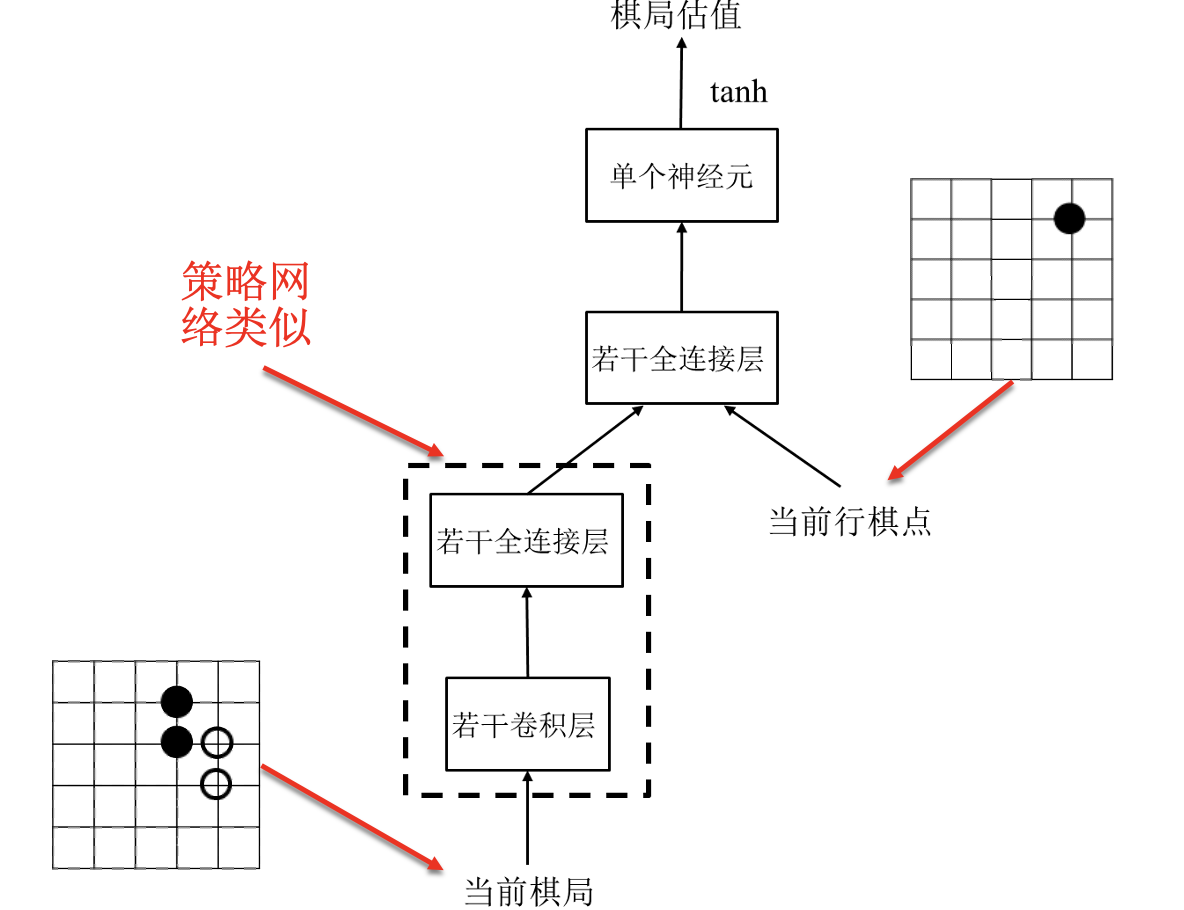
- 估值网络: 由一个神经网络构成.
  - 输入: 当前棋局 —— 49 个通道, 每个通道大小为 19*19.
  - 输出: 当前棋局的收益 —— 收益的取值范围为 $[-1, 1]$.
  - 训练数据: 16 万盘人类棋手的数据.
  - 回归问题: 获胜时收益为 $1$, 失败时收益为 $-1$.
  - 损失函数:
    $L(w)=(R-V(s))^2.$
    其中 $R$ 为棋局的胜负, 胜为 1, 负为 -1; $V(s)$ 为估值网络的输出, 即预测的收益.
- MCTS 中的选择原则:
  - 利用: 收益好的节点.
  - 探索: 模拟次数少的节点.
  - 经验: 落子概率高的节点 (AlphaGo 增加的第三个原则).
- 节点 $s$ 第 $i$ 次模拟的收益:
  $v_i(s)=\lambda value(s)+(1-\lambda)rollout(s).$
  其中 $value(s)$ 是估值网络的输出, $rollout(s)$ 是一次模拟结果.
- 平均收益:
  $Q(s_a)=\dfrac{1}{n}\sum\limits_{i=1}^{n}v_i(s_a).$
  其中 $s(a)$ 为 $s$ 棋局下在 $a$ 处落子后的棋局.
- 探索项:
  $u(s_a)=c\cdot p(s_a)\dfrac{\sqrt{N(s)}}{N(s_a+1)}.$
  其中 $N(\cdot)$ 为模拟次数, $p(s_a)$ 为策略网络在 $a$ 处下棋概率, $c$ 为加权系数.
AlphaGo 中的 MCTS 过程:
- 用 $Q(s_a)+u(s_a)$ 代替信心上限 $I_j$, 优先选择 $Q(s_a)+u(s_a)$ 大的子节点.
- 遇到叶节点 $s_l$ 结束, 该节点被选中.
- 生成 $s_l$ 的所有子节点, 但是不进行模拟.
- 规定了最大节点深度.
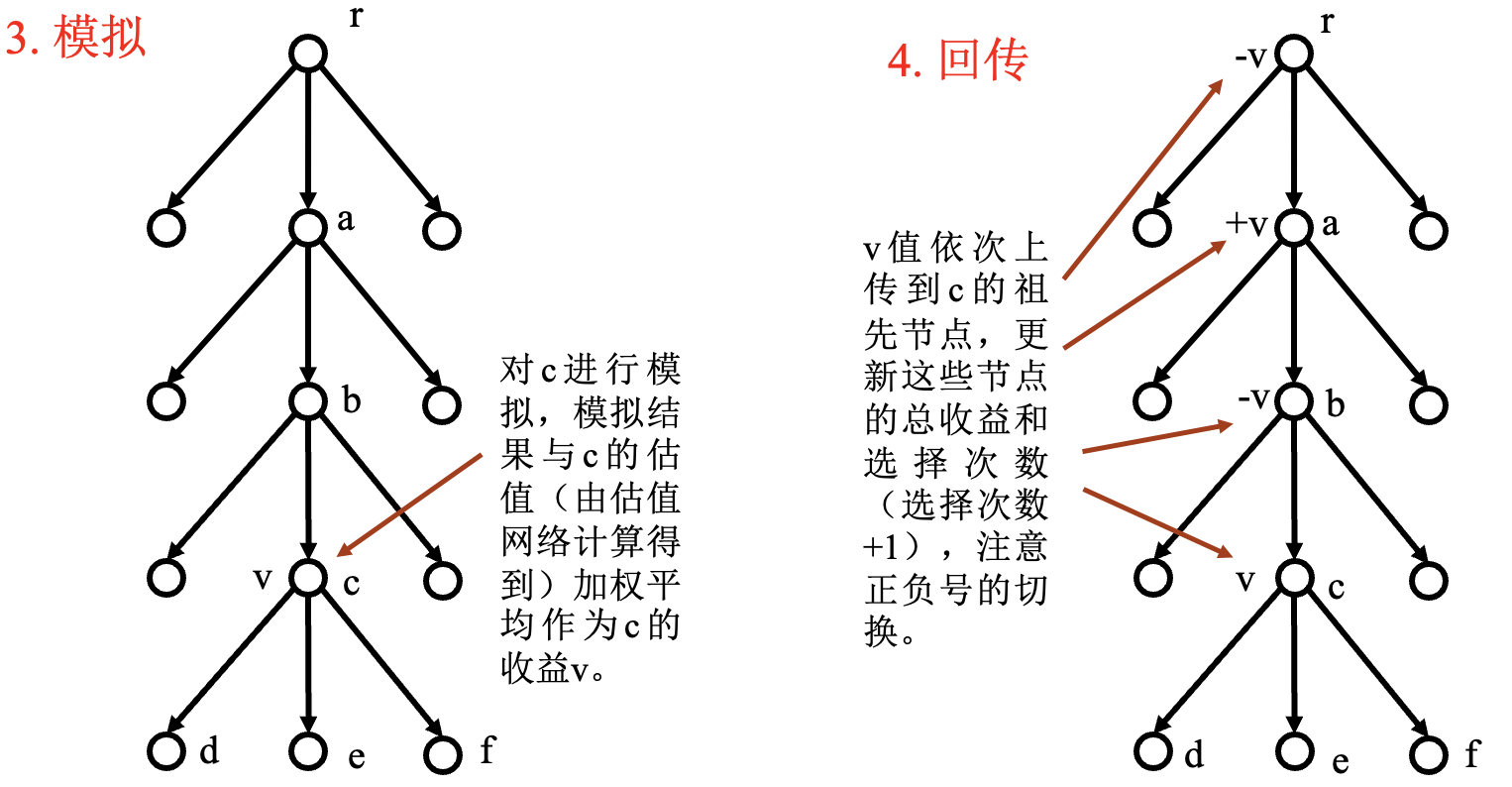
- 对 $s_l$ 进行模拟, 计算:
  $v_i(s)=\lambda value(s)+(1-\lambda)rollout(s).$
- 模拟过程采用推演策略网络, 其速度快, 是策略网络的 $1000$ 倍.
- 规定了总模拟次数.

围棋中的深度强化学习方法

强化学习:
- 学习 “做什么才能使得收益最大化” 的方法.
- 学习者不会被告知如何做, 必须自己通过尝试发现哪些动作会产生最大的收益.
- 监督学习使用策略网络、无需尝试.
- 两个特征: 试错和延迟收益.
深度强化学习:
- 用深度学习 (神经网络) 方法实现的强化学习.
关键问题: 如何获得指示信号?
- 监督学习: 情景与标注一一对应.
- 强化学习:
  - 将收益转化为 “标注”.
  - 不能获得所有情况下既正确又有代表性的示例.
手段:
- 将深度强化学习问题转化为神经网络训练问题.
- 不同的转换方法构成了不同的深度强化学习方法.
- 关键是损失函数的定义.
围棋中深度强化学习的三种实现方法:
- 基于策略梯度的强化学习:
  - 数据: $(s,a,p_a,t_a)$ (棋局、行棋、获胜概率、延迟胜负值).
    
    $t_a$ 为胜负值, 胜为 1, 负为 -1.
  - 损失函数: $L(w)=-t_a\log⁡(p_a)$.
    - 假设获胜者的行为都是正确的, 负者行为都是不正确的.
    - 假设获负时对权重的修改量大小与获胜时一样, 方向相反.
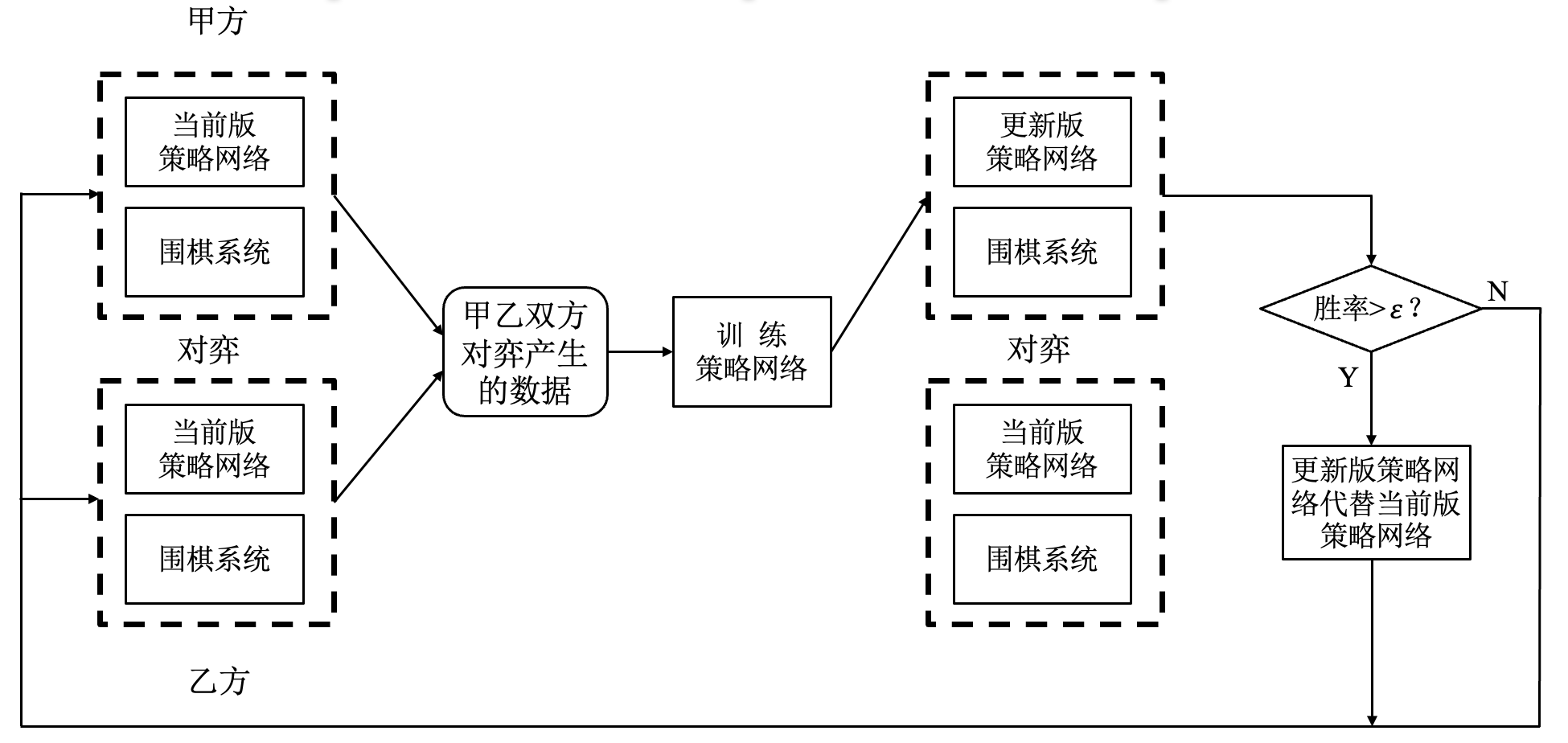
  - AlphaGo: 先监督学习, 再强化学习.
  - 注意点:
    - 强化学习过程中, 每个样本只使用一次;
    - 基于策略梯度的强化学习学到了在每个可落子点行棋的获胜概率; 监督学习学到了在某个可落子点的行棋概率.
- 基于价值评估的强化学习:
  - 输入: 当前棋局和行棋点.
  - 输出: 取值在 -1、1 之间的估值.
  - 数据: $(s,a,V(s,a),R)$ (棋局、行棋、网络输出、延迟胜负值).
    
    $R$ 为胜负值, 胜为 1, 负为 -1.
  - 损失函数: $L(w)=(E-V(s,a))^2$.
  - 基于价值评估的强化学习学到了每个落子点获取最大收益的概率.
- 基于演员-评价方法的强化学习:
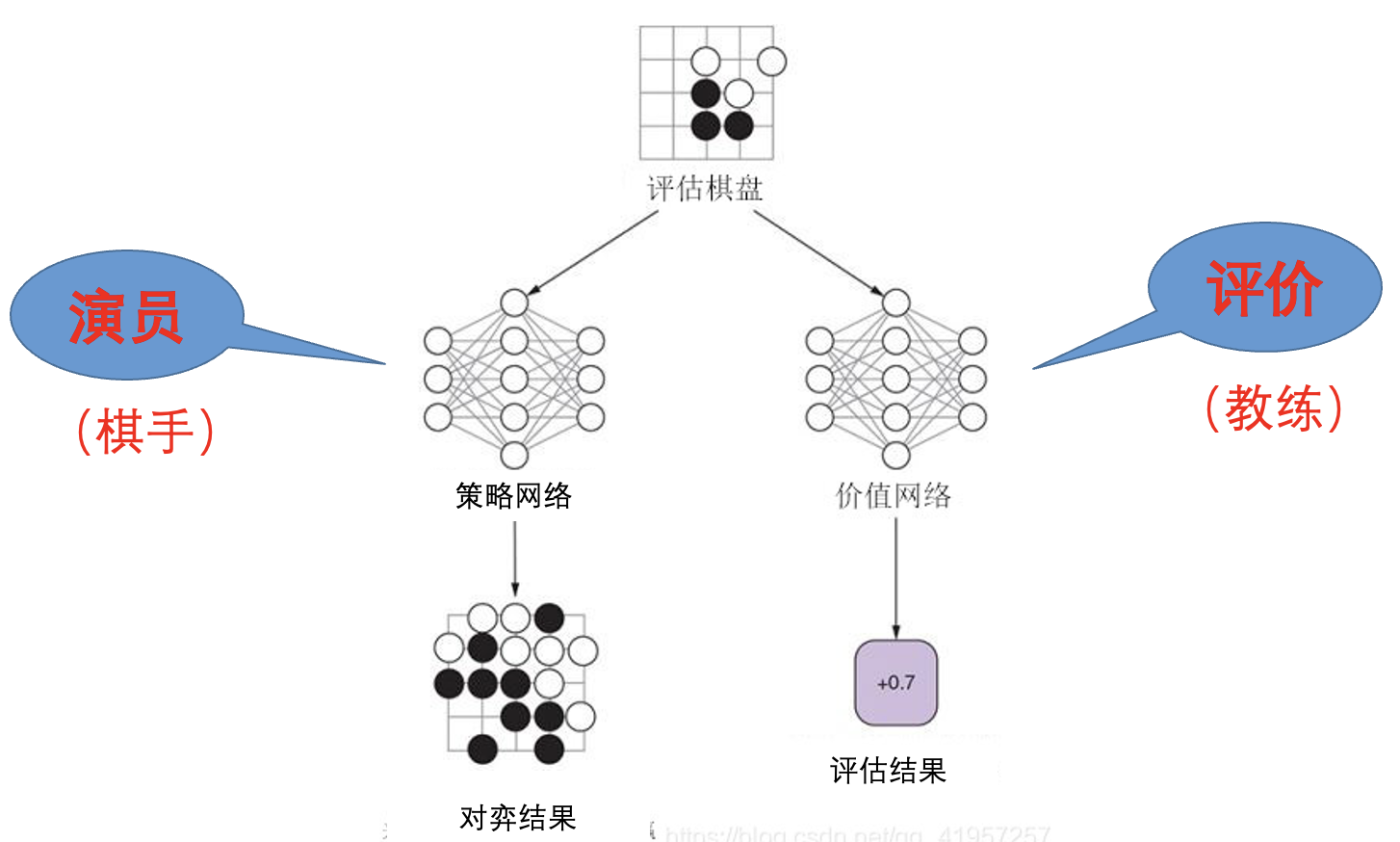
  - 收益增量:
    - 评价一步棋的好坏
      $A=Q(s,a)-V(s).$
    - $V(s)$ 为棋局 $s$ 的预期收益, 取值范围为 $[-1, 1]$.
    - $Q(s,a)$ 为在 $a$ 处行棋后的收益, 取值范围为 $[-1, 1]$.
    - $A$ 为收益增量, 取值范围为 $[-2, 2]$.
    - $A$ 越大越说明走了一步妙招, 越小越说明走了一步败招.
  - 收益增量的计算:
    $A=R-V(s).$
    其中 $R$ 为胜负值, 胜为 $1$, 负为 $-1$.
  - 损失函数:
    - 评价部分: $L_1(w)=(R-V(s))^2$.
    - 演员部分: $L_2(w)=-\vert A\vert t_a\log(p_a)=-A\log(p_a)$.
    - 综合损失函数: $L(w)=L_1(w)+\lambda L_2(w)$.
  - 基于演员-评价方法的强化学习强调重要行棋点的学习, 学到了每个落子点获取最大收益增量的概率.

AlphaGo Zero 原理

从零学习:
- 不再使用人类棋手的数据.
- 不再使用人工特征作为输入 (自动抽取).
- 利用强化学习从零学习.
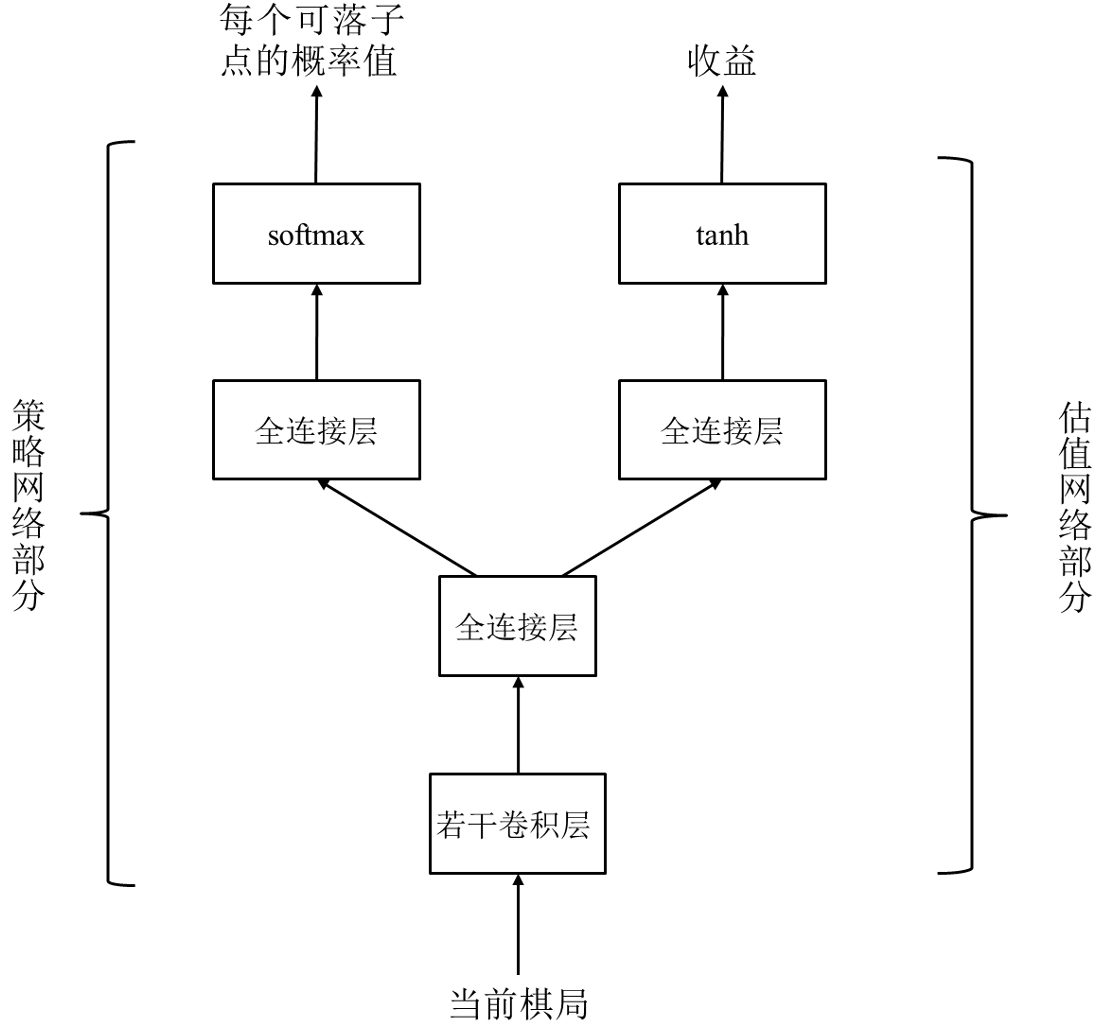
AlphaGo Zero 的网络结构:
- 将策略网络、估值网络合并为一个 “双输出” 网络.
- 输入: 17 个通道, 每个通道大小为 19*19.
- 策略网络输出: 19×19+1, 多了一个 “放弃” 行为.
- 估值网络输出: 当前棋局的估值, 取值范围为 $[-1, 1]$.
AlphaGo Zero 中的 MCTS:
- 节点 $s$ 第 $i$ 次模拟的收益 (AlphaGo $\Rightarrow$ AlphaGo Zero):
  $v_i(s)=\lambda value(s)+(1-\lambda)rollout(s)\Rightarrow v_i(s)=value(s).$
  其中 $value(s)$ 是估值网络的输出.
- 平均收益:
  $Q(s_a)=\dfrac{1}{n}\sum\limits_{i=1}^{n}v_i(s_a).$
  其中 $s(a)$ 为 $s$ 棋局下在 $a$ 处落子后的棋局.
- 探索项:
  $u(s_a)=c\cdot p(s_a)\dfrac{\sqrt{N(s)}}{N(s_a+1)}.$
  其中 $N(\cdot)$ 为模拟次数, $p(s_a)$ 为策略网络在 $a$ 处下棋概率, $c$ 为加权系数.
AlphaGo Zero 中的 MCTS 过程:
- 选择:
  - 用 $Q(s_a)+u(s_a)$ 代替信心上限 $I_j$, 选择 $Q(s_a)+u(s_a)$ 大的子节点;
  - 遇到叶节点 $s_l$ 结束, 该节点被选中.
- 生成:
  - 生成 $s_l$ 的所有子节点, 但是不进行模拟;
  - 规定了最大节点深度.
- 模拟回传:
  - 用估值网络输出取代快速模拟过程, 对 $s_l$ 进行模拟, 计算:
    $v_i(s)=value(s).$
  - 规定了总模拟次数.
损失函数:
- 估值网络部分:
  $L_1=(z-v)^2.$
  其中 $v$ 是估值网络的输出, $z$ 是胜负值.
- 策略网络部分:
  $L_2=-\sum_{i=1}^{362}\pi_i\log(p_i).$
  其中 $\pi(i)$ 是 MCTS 输出的每个落子点的概率 (与每个点被选中次数有关), $p_i$ 是策略网络输出的每个落子点的概率.
- 综合损失函数:
  $L=L_1+L_2+\Vert\theta\Vert_2^2.$
  其中 $\Vert\theta\Vert_2^2$ 防止出现过拟合.
引入多样性:
- 防止走向错误的方向, 对策略网络的输出人为引入噪声.
- 狄利克雷分布:
  - 通过参数可以产生一些符合一定条件的概率分布.
  - 控制参数 $n$ 概率分布向量的长度与 $\alpha$ 分布浓度.
- 落子概率:
  $p=\lambda p_a+(1-\lambda)p_d.$
  其中 $p_a$ 为策略网络输出, $p_d$ 为狄利克雷分布采样.
- 引入噪声不会引起 “不良反应”, MCTS 具有 “纠错” 能力.