分类问题
有一个判断性别的机器学习模型, 使用它来判断「是否为男性」时, 会出现 4 种情况:

这 4 种情况构成了混淆矩阵:
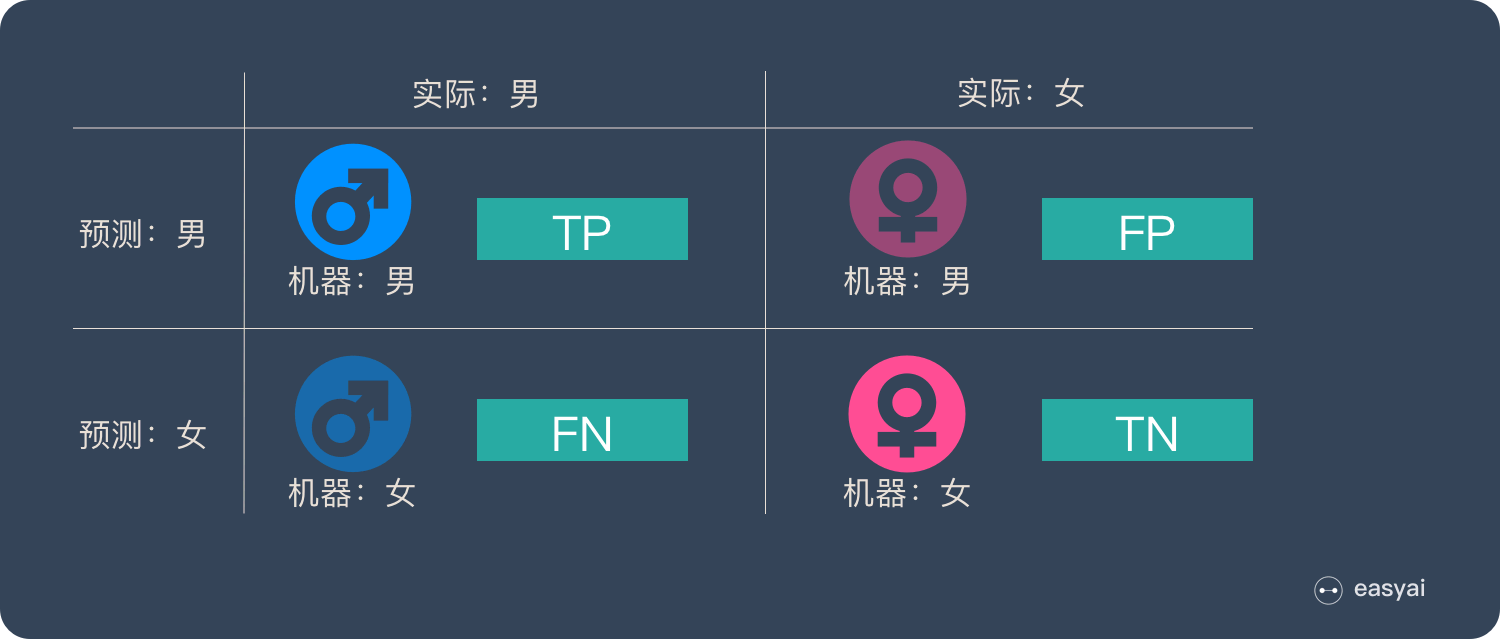
其中 T/F 描述机器判断结果的正确性, P/N 描述机器判断分类的正负性.
基础分类指标
准确率 Accuracy
准确率为预测正确的结果占总样本的百分比:
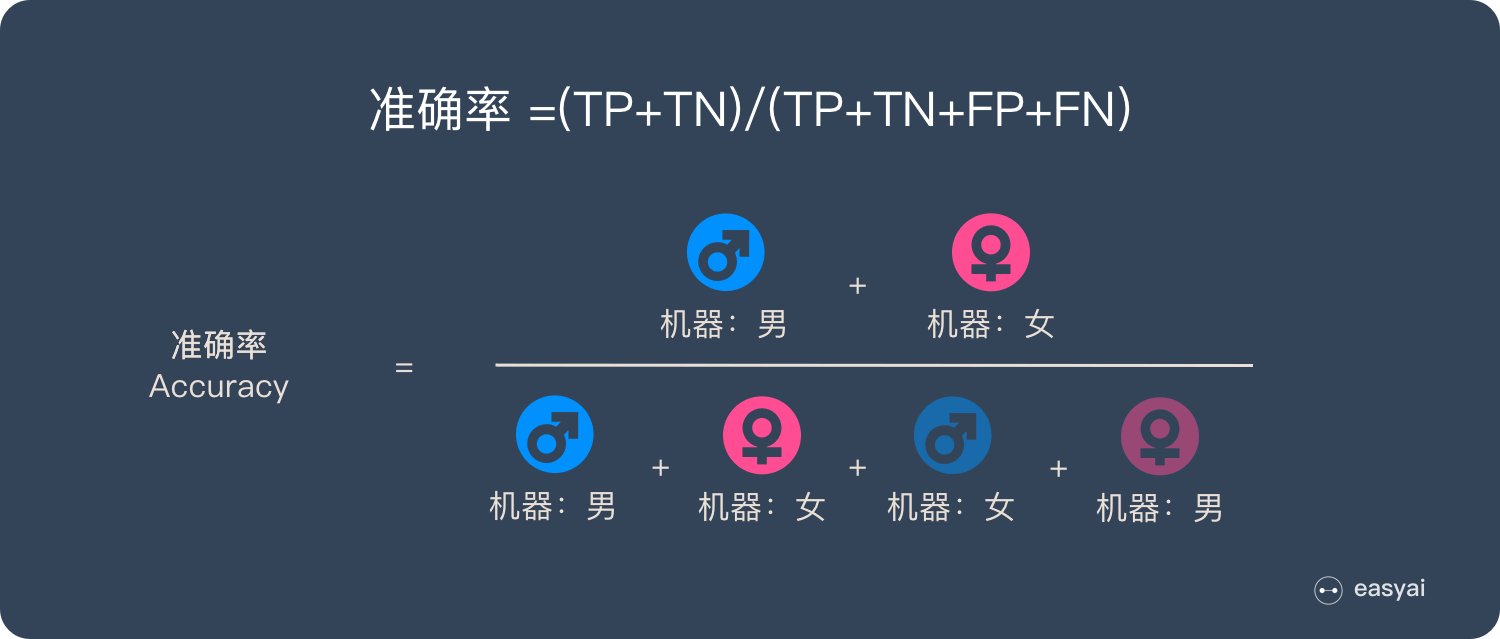
可以判断总的正确率, 但是在样本不平衡的情况下, 不能作为指标来衡量结果. 在正样本占 90%, 负样本占 10% 的总样本中, 样本严重不平衡. 这种情况只需将全部样本预测为正即可得到 90% 的准确率, 结果含有水分, 准确率失效.
查准率 Precision
查准率为所有被预测为正的样本中实际为正的样本的概率:
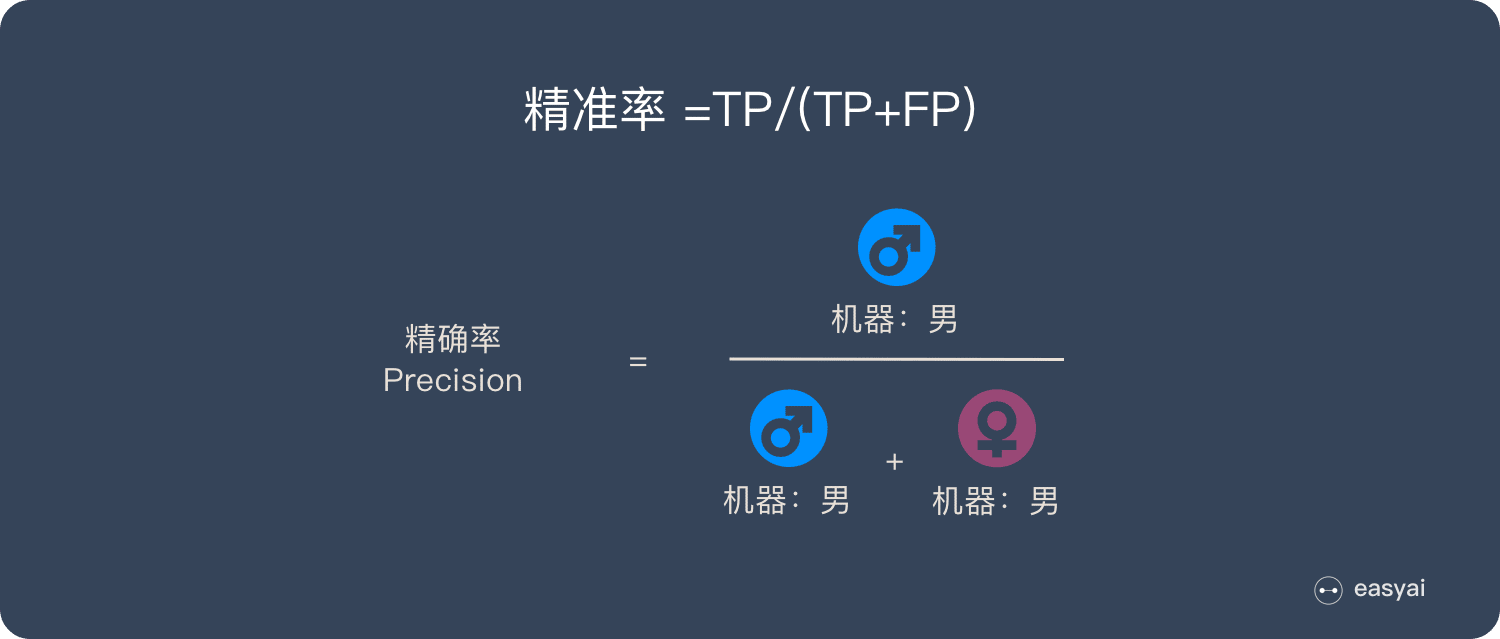
查准率代表对正样本结果中的预测准确程度, 有多少把握预测正确; 而准确率则代表整体的预测准确程度, 包括正样本和负样本.
查全率 Recall
查全率为所有实际为正的样本中被预测为正的样本的概率:
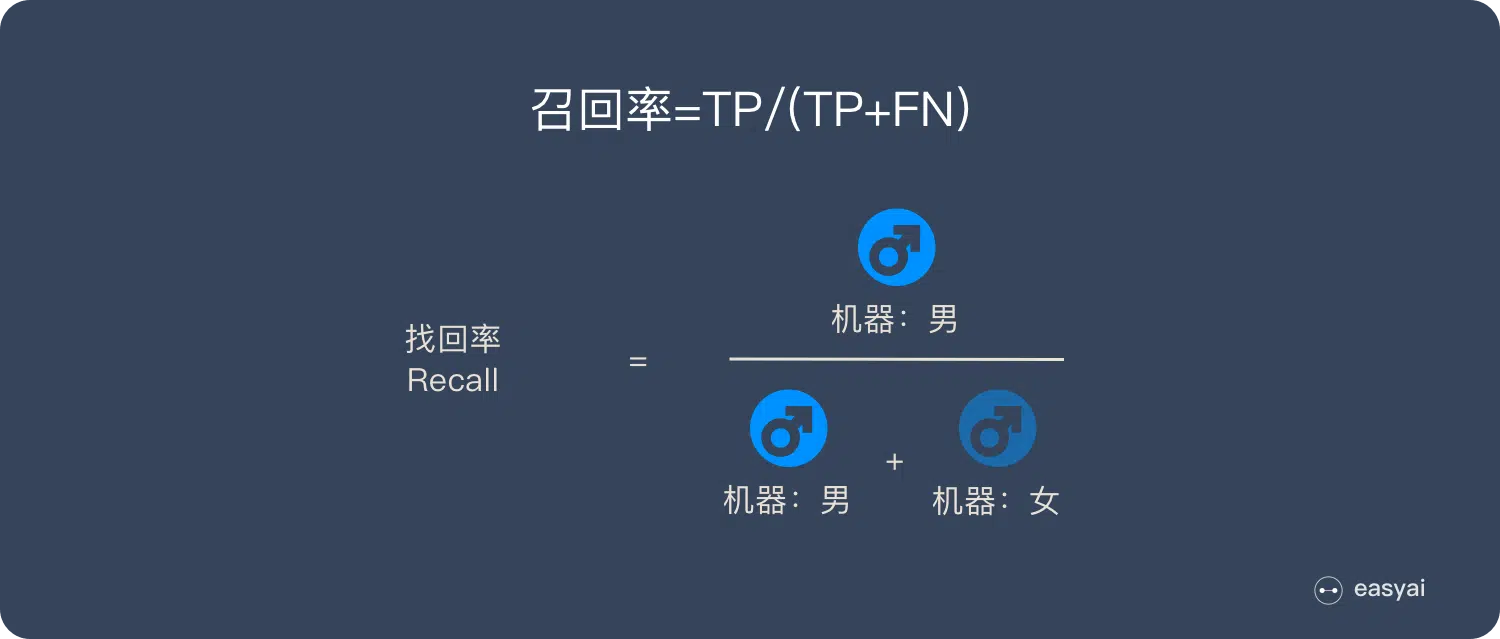
查全率越高, 代表实际用户被预测出来的概率越高.
F1分数 F1$_$Score
Precision 和 Recall 之间的关系用 P-R 曲线来表达:
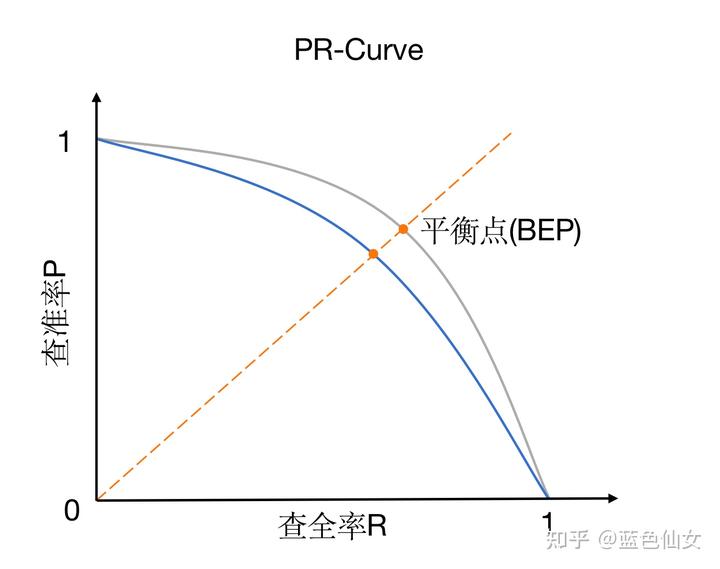
以逻辑回归举例, 输出是一个 0 到 1 之间的概率数字, 根据这个概率判断用户好坏, 必须定义一个阈值. 为了找到一个最合适的阈值满足我们的要求, 必须遍历 0 到 1 之间所有的阈值, 每个阈值下都对应着一对 Precision 和 Recall, 从而得到了这条曲线.
想要找到二者之间的平衡点, 就需要一个新的指标 F1$_$Score. F1$_$Score 同时考虑了 Precision 和 Recall, 让二者同时达到最高, 公式为:
P-R 曲线的两个指标都聚焦于正样本, 适合评估在相同的类别分布下正例的预测情况.
样本不平衡处理
灵敏度 Sensitivity/特异度 Specificity/真正率 TPR/假正率 FPR
以下指标能无视样本不平衡:
Sensitivity 为实际为正的样本被预测为正的概率, Specificity 为实际为负的样本被预测为负的概率. 由于关心正样本, 所以使用 1 - Specificity, 查看负样本被错误预测为正的概率.
TPR 和 FPR 分别从实际表现的各个结果角度出发, 在实际的正样本和负样本中来观察相关概率, 无论样本是否平衡, 都不会被影响. TPR 只关注正样本中有多少被真正覆盖, FPR 只关注负样本中有多少被错误覆盖的.
从「条件概率」说起
假设 X 为预测值, Y 为真实值, 可以将这些指标按条件概率表示:
如果先以实际结果为条件 (Recall/Sensitivity/Specificity), 就只需考虑一种样本; 而先以预测值为条件 (Precision), 需要同时考虑正样本和负样本. 所以先以实际结果为条件的指标都不受样本不平衡的影响, 相反以预测结果为条件就会受到样本不平衡的影响.
接受者操作特征曲线 ROC
ROC 曲线的横坐标为假正率 FPR, 纵坐标为真正率 TPR:
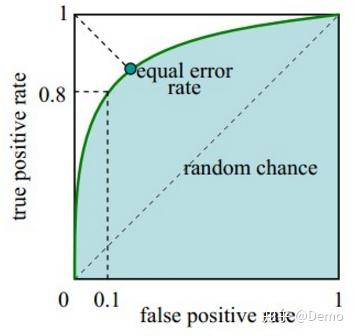
与 P-R 曲线类似, ROC 曲线也通过遍历所有阈值来绘制:
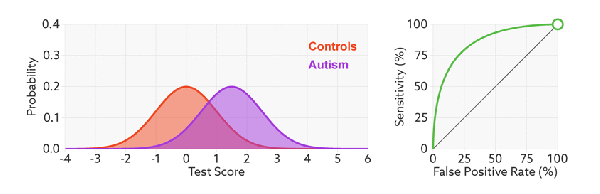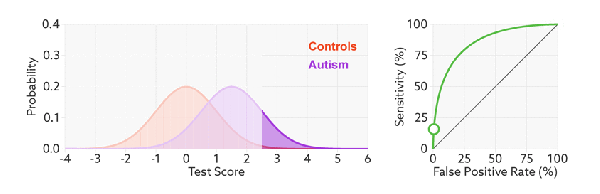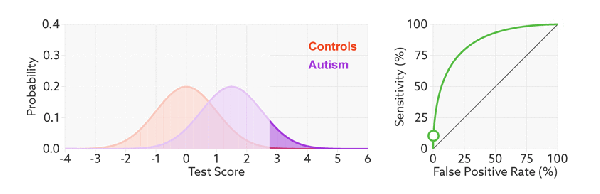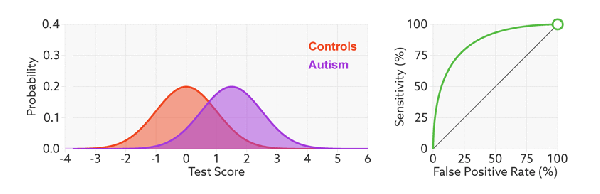
改变阈值只是改变预测的正负样本数, 即 TPR 和 FPR, 但是曲线本身不变. FPR 表示模型虚报的响应程度, 而 TPR 表示模型预测响应的覆盖程度. TPR 越高, 同时 FPR 越低, 即 ROC 曲线越陡, 那么模型性能越好:
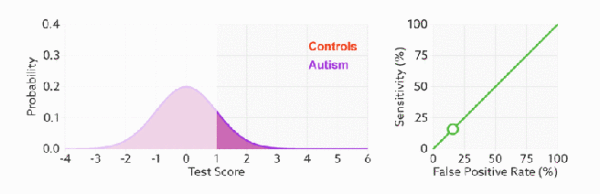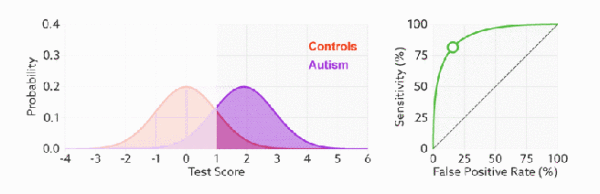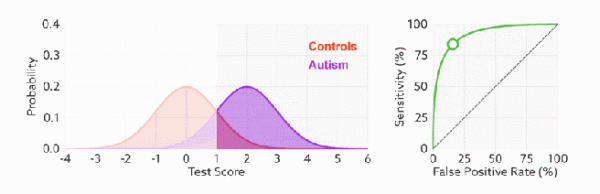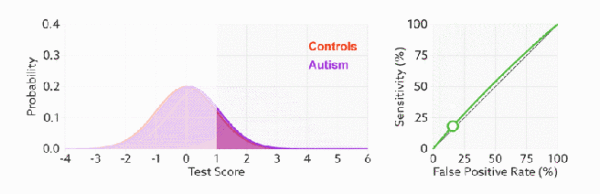
当测试集中的正负样本的分布变化时, TPR 和 FPR 能无视样本不平衡, ROC 曲线聚焦于整体, 保持不变, 使其成为较均衡的评估方法.
曲线下面积 AUC
为了计算 ROC 曲线上的点, 可以使用不同的分类阈值多次评估逻辑回归模型, 但效率非常低. 一种基于排序的高效算法可以提供此类信息, 称为 AUC.
可以断言, AUC 越大, 模型效果越好. 随机判断响应与否, 正负样本覆盖率都是 50%, 表示随机效果, 对应的 ROC 曲线即对角线. 在最坏情况下总有 TPR=FPR, 即 AUC = 0.5; 如果AUC < 0.5, 只要取反预测类别, 便得到了 AUC > 0.5 的分类器.



