第四章统计机器学习

统计机器学习

如果一个系统能够通过执行某个过程改进它的性能, 这就是学习.
统计学习就是计算机系统通过运用数据及统计方法提高系统性能的机器学习.
统计学习从数据出发, 提取特征, 抽象模型, 发现知识, 回到分析与预测.
统计学习的目标就是考虑学习什么样的模型和如何学习, 以使模型能对数据进行准确的预测和分析, 具有优秀的理论基础与可解释性.

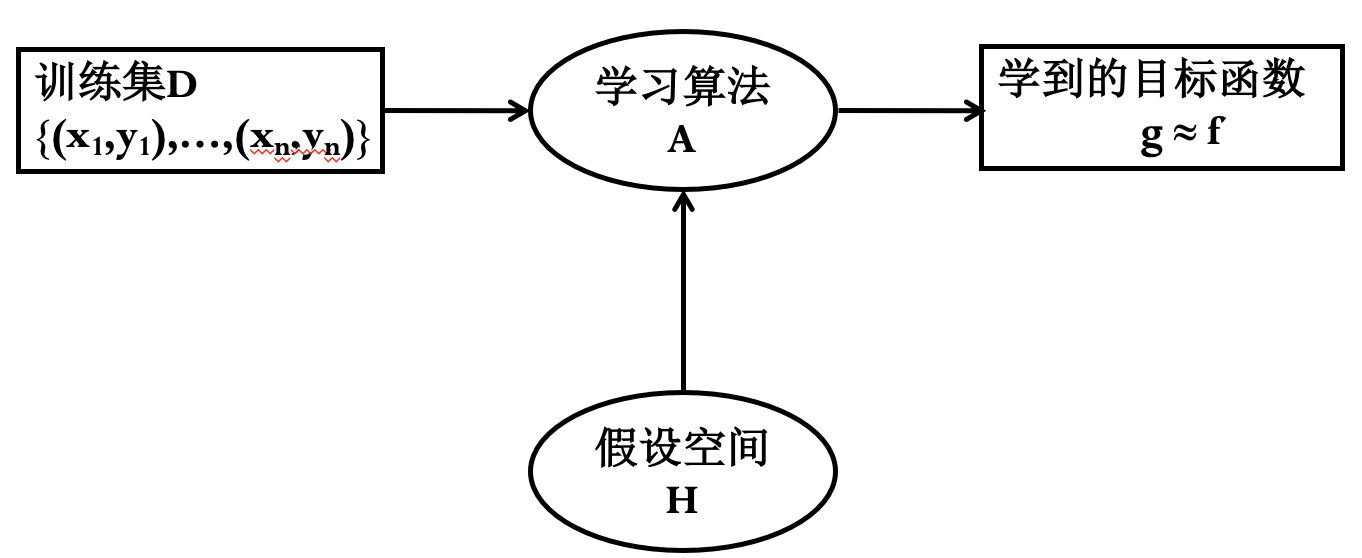
其中 $x_i$ 为特征, $y_i$ 为标签. 学习算法 A 根据训练集 D 从假设空间 H 中选择一个最好的 $g\approx f$.
统计学习三要素:
- 模型: 学习什么样的模型.
  - 条件概率分布、决策函数.
- 策略: 模型选择的准则.
  - 经验风险最小化、结构风险最小化.
- 算法: 模型学习的算法.
  - 一般归结为一个最优化问题.
统计机器学习分类:
- 监督学习: 有标签、人为标注 (汉字识别、动物识别).
- 非监督学习: 无标签 (图片归类).
- 自监督学习: 非监督学习的一种 (神经网络语言模型).
- 半监督学习: 综合监督与非监督学习.
- 弱监督学习: 强化学习 (围棋训练).

支持向量机 (SVM)

定义:
- 二类分类器: 经过组合可解决多分类问题.
- 特征空间上的间隔最大化线性分类器.
- 通过核技巧可实现非线性分类.
- 根据模型的复杂程度划分.
线性可分支持向量机:

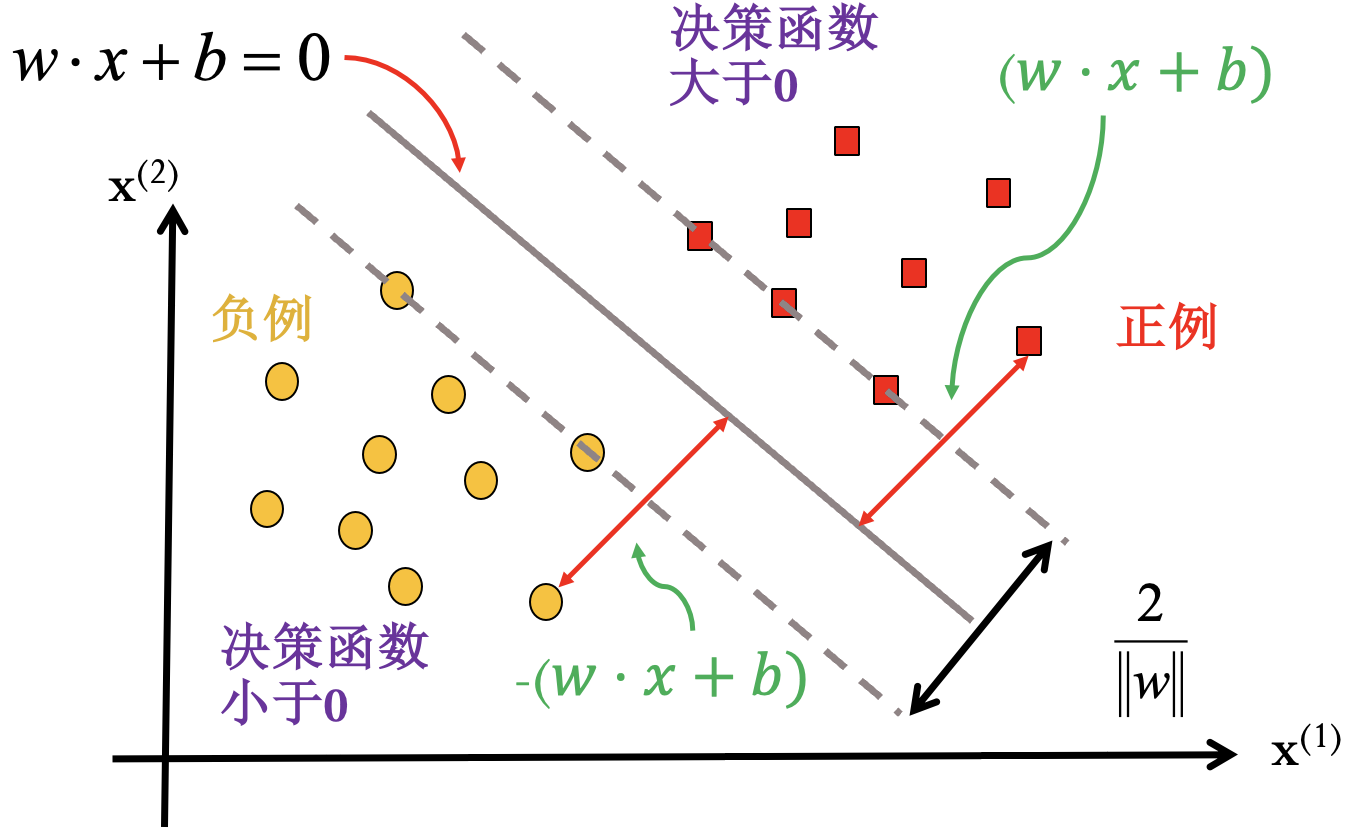
通过间隔最大化得到分类超平面:
$w^*\cdot x+b^*=0.$
相应的决策函数:
$f(x)=sign(w^*\cdot x+b^*).$
函数间隔:
$\hat\gamma_i=y_i(w\cdot x_i+b)\Rightarrow\hat\gamma=\min_{i}\hat\gamma_i.$
几何间隔:
$\gamma_i=y_i(\dfrac{w}{\Vert w\Vert}\cdot x_i+\dfrac{b}{\Vert w\Vert})\Rightarrow\gamma=\min_{i}\gamma_i.$
间隔最大化问题:
$\max_{w,b}\gamma\quad s.t.\quad y_i(\dfrac{w}{\Vert w\Vert}\cdot x_i+\dfrac{b}{\Vert w\Vert})\ge\gamma,\,1\le i\le N.$
转化为凸二次规划问题:
$\min_{w,b}\dfrac{1}{2}\Vert w\Vert^2\quad s.t.\quad y_i(w\cdot x_i+b)\ge 1,\,1\le i\le N.$
定义拉格朗日函数:
$L(w,b,\alpha)=\dfrac{1}{2}\Vert w\Vert^2+\sum_{i=1}^{N}\alpha_i[1-y_i(w\cdot x_i+b)],\,\alpha_i\ge 0,\,1\le i\le N.$
下列命题与原命题等价:
$\min_{w,b}\max_{\alpha}L(w,b,\alpha).$
满足KKT条件时, 对偶命题与原命题等价:
$\min_{w,b}\max_{\alpha}L(w,b,\alpha)=\max_{\alpha}\min_{w,b}L(w,b,\alpha).$
对 $w, b$ 求偏导令其为 0 并代入, 得到对偶问题:
$\min_{\alpha}\Big(\dfrac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^{N}\alpha_i\Big)\quad s.t.\quad \sum_{i=1}^{N}\alpha_iy_i=0.$
获得 $w^,b^$:

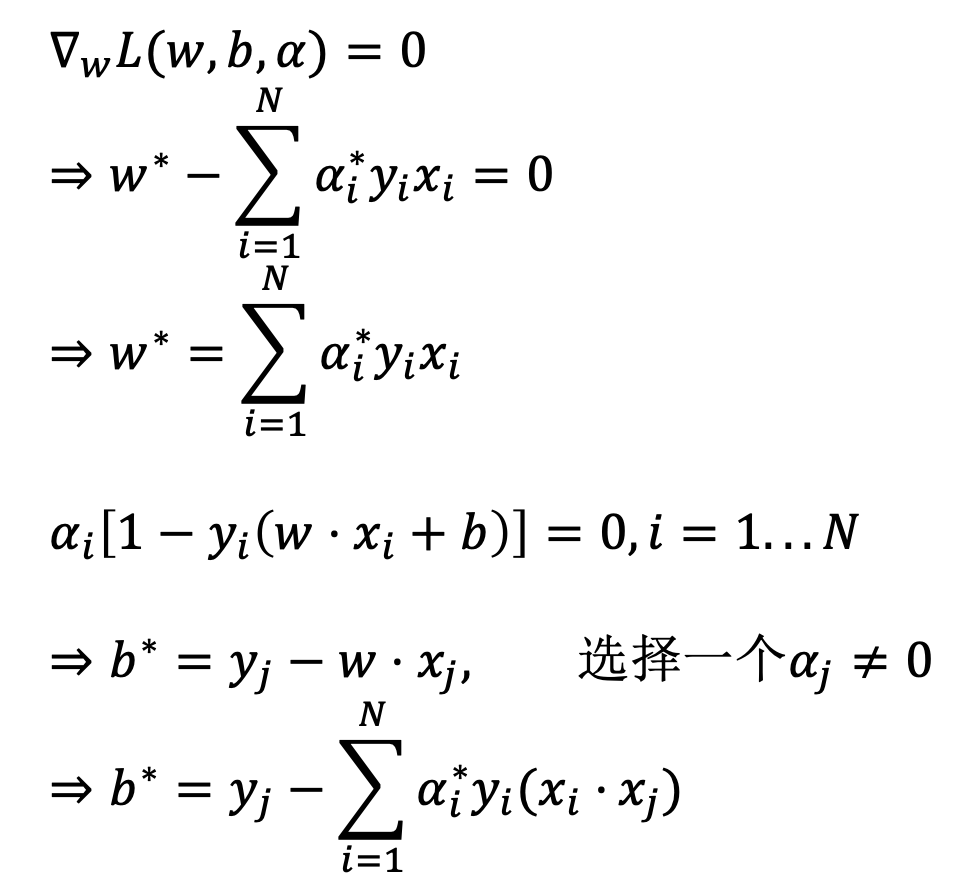
与 $\alpha_i>0$ 对应的实例 $x_i$ 就是支持向量.
线性支持向量机:

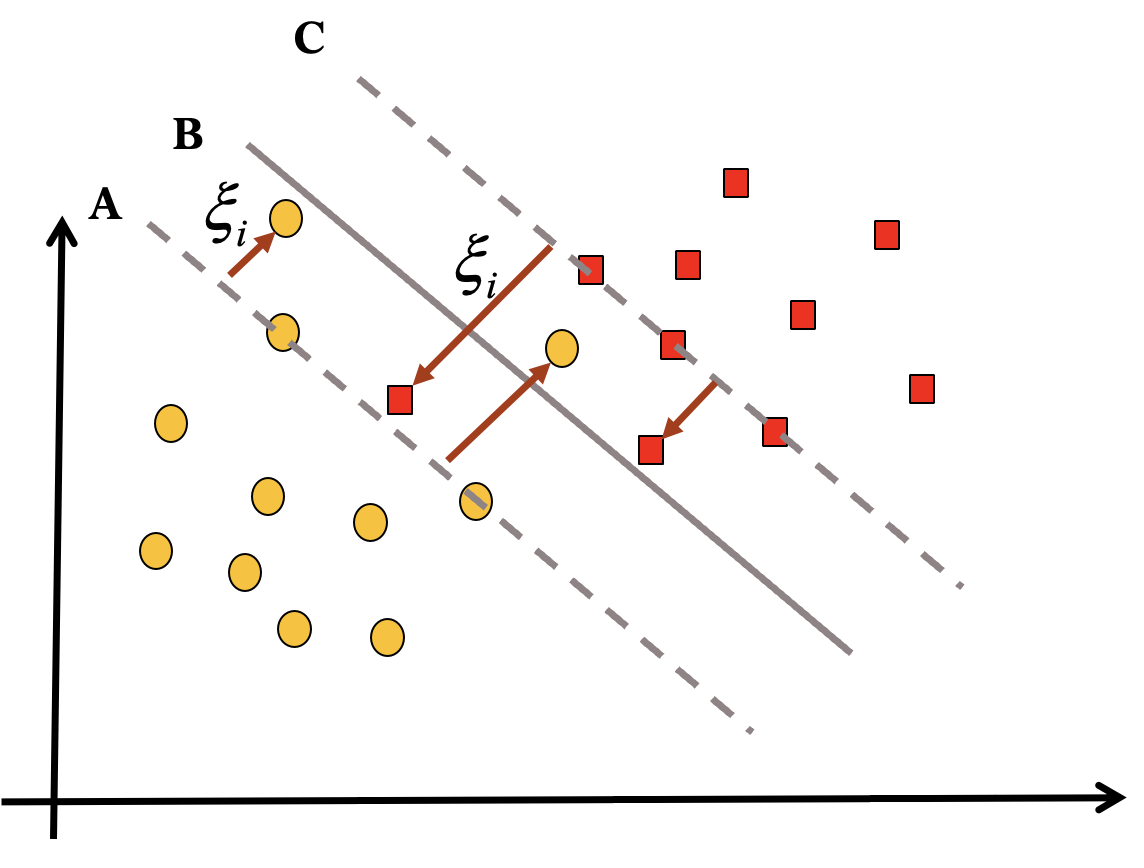
转化为凸二次规划问题:
$\min_{w,b}(\dfrac{1}{2}\Vert w\Vert^2+C\sum_{i=1}^{N}\xi_i)\quad s.t.\quad y_i(w\cdot x_i+b)\ge 1-\xi_i,\,1\le i\le N.$
得到对偶问题:
$\min_{\alpha}\Big(\dfrac{1}{2}\sum_{i,j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^{N}\alpha_i\Big)\, s.t.\,0\le\alpha_i\le C, \sum_{i=1}^{N}\alpha_iy_i=0.$
获得 $w^,b^$:

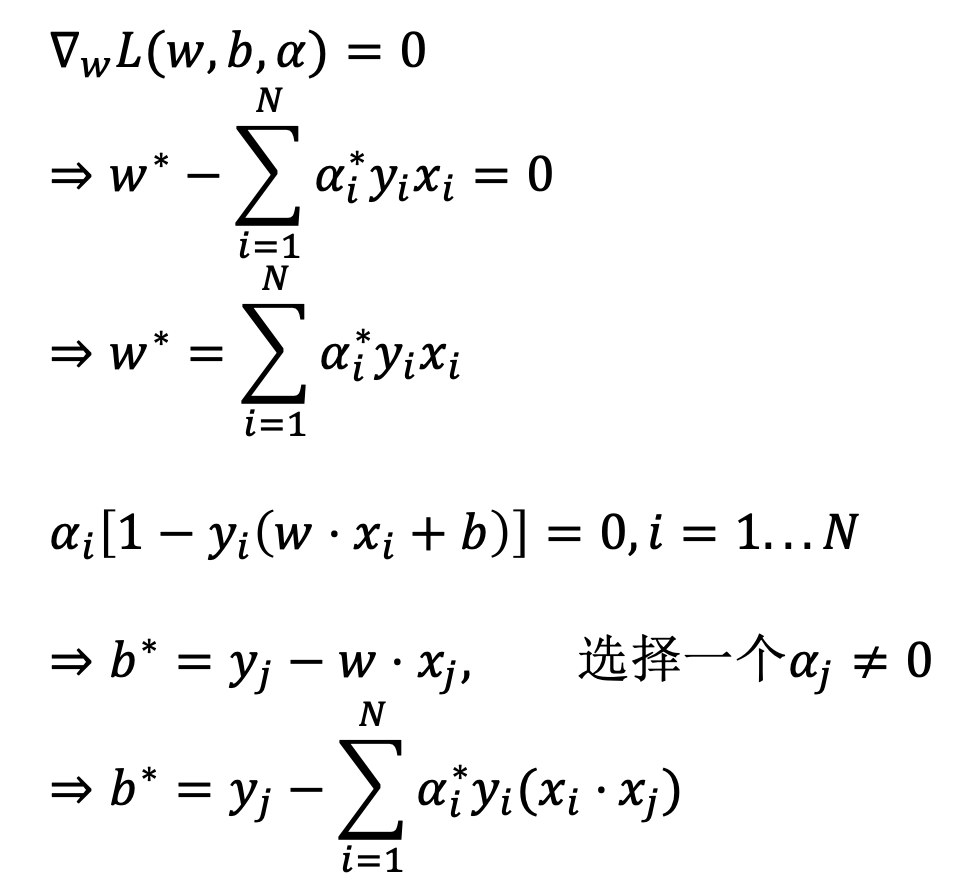
与 $\alpha_i>0$ 对应的实例 $x_i$ 就是支持向量.
非线性支持向量机:

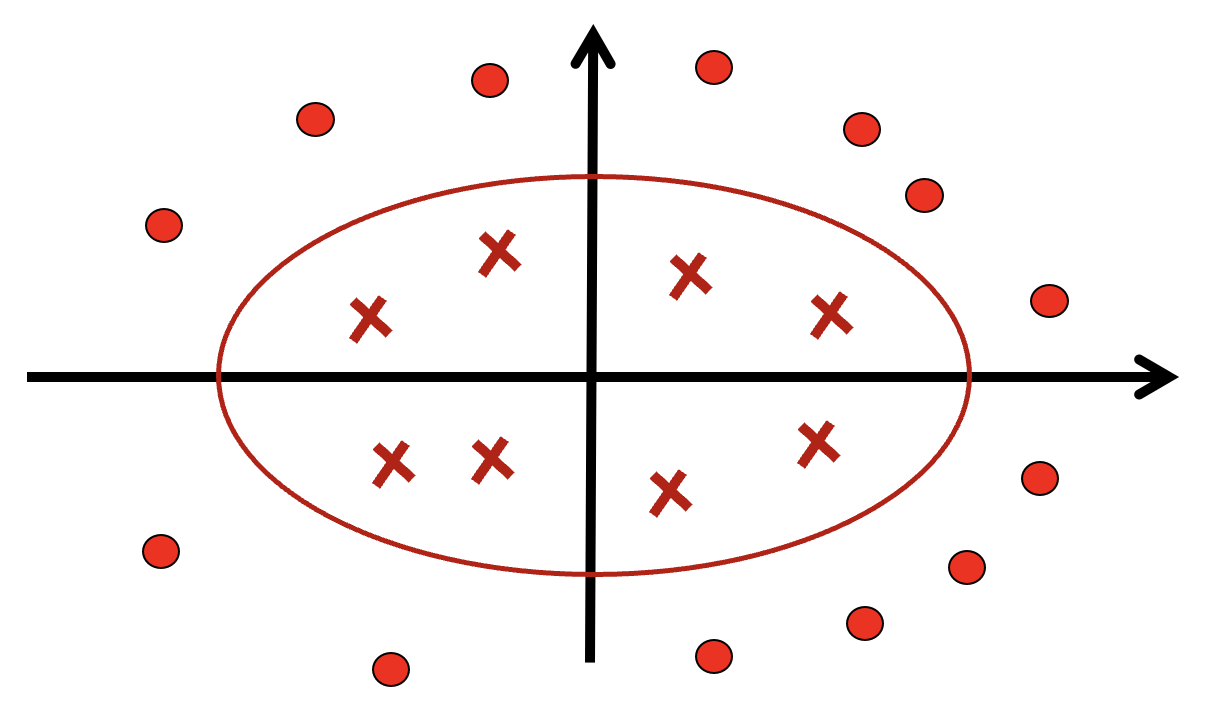
利用变换:

将原空间的椭圆:

变换为新空间的直线:

通过一个非线性变换将输入空间 $X$ 对应于一个特征空间 $H$ 使, 得在输入空间 $X$ 的超曲面模型对应于特征空间 $H$ 中的超平面模型. 分类问题的学习就可以通过在 $H$ 空间中求解线性支持向量机完成.

得到对偶问题:

常见核函数为:
- 内积核函数
  $K(x,z)=(x\cdot z)^2.$
- 多项式核函数
  $K(x,z)=(x\cdot z+1)^p.$
- 高斯核函数
  - $\sigma$ 过大: 欠拟合;
  - $\sigma$ 恰当: 恰拟合;
  - $\sigma$ 过小: 过拟合.
  得到最终对偶问题:
  
  获得 $w^,b^$:
  
  其中 $w$ 无法直接得到, 此时情况为超曲面.
序列最小最优化算法 SMO:
- 支持向量机的学习问题是一个凸二次规划问题, 具有全局最优解.
- 是一种快速算法.
SVM求解多类问题:
- 一对多: 某类为正例, 其余类为负例. 分类时将未知样本分类为具有最大分类函数值的那类 (样本不均衡).
- 一对一: 任两类构造 SVM, 采取投票法决定类别 (效果好、数量大).
- 层次法: 所有类先分成两类, 每类再分为两类, 以此类推.

决策树

对实例分类的树形结构. 内部节点表示一个特征或属性, 叶节点表示一个类.
决策树学习:
- 从训练集归纳出分类规则, 得到与训练集矛盾较小的决策树.
- 对给定训练集, 可构造多个决策树, 以损失函数最小化作为优化目标.
- 选取最优决策树是一个 NPC 问题, 一般采用启发式方法得到近似解.
决策树学习——特征选择:
- 按照信息增益选择特征.
- 熵表示数据的混乱程度, 条件熵表示已知条件下数据的不确定性.
  - 随机变量 $X$ 的熵:
    $H(X)=-\sum_{i=1}^{n}p_i\log p_i.$
    当条件由数据集 $D$ 估计得到时, 记为 $H(D)$.
  - 条件熵:
    $H(Y\mid X)=\sum_{i=1}^{n}p_iH(Y\mid X=x_i).$
    表示已知 $X$ 时 $Y$ 的不确定性.
- 信息增益是特征 A 对数据集 D 进行分类不确定性的减少程度.
  $g(D,A)=H(D)-H(D\mid A).$
  信息增益大的特征具有更强的分类能力.
- 设训练集 $D$, $K$ 个类 $C_k$, 特征 $A$ 有 $n$ 个不同的取值 $\{a_1,\cdots,a_n\}$. $A$ 的不同取值将 $D$ 划分为 $n$ 个子集 $D_1$, $\cdots$, $D_n$, $D_i$ 中属于类 $C_k$ 的样本的集合为 $D_{ik}$, $\vert\cdot\vert$ 表示样本个数. 计算信息增益:
  $H(D)=-\sum_{k=1}^{K}\dfrac{\vert C_k\vert}{\vert D\vert}\log_2\dfrac{\vert C_k\vert}{\vert D\vert}.\\ H(D\mid A)=\sum_{i=1}^{n}\dfrac{\vert D_i\vert}{\vert D\vert}H(D_i)=-\sum_{i=1}^{n}\dfrac{\vert D_i\vert}{\vert D\vert}\sum_{k=1}^{K}\dfrac{\vert D_{ik}\vert}{\vert D_i\vert}\log_2\dfrac{\vert D_{ik}\vert}{\vert D_i\vert}.$
决策树学习——决策树的生成:
- ID3 算法:
  - 输入: 训练集 $D$, 特征集 $A$, 阈值 $\varepsilon$ >0.
  - 输出: 决策树 $T$.
  1. 若 $D$ 中所有实例属于同一类 $C_k$, 则 $T$ 为单节点树, $C_k$ 为该节点类标记, 返回 $T$.
  2. 若 $A$ 为空, 则 $T$ 为单节点树, $D$ 中实例数最大的类 $C_k$ 为该节点类标记, 返回 $T$.
  3. 否则计算 $A$ 中各特征对 $D$ 的信息增益. 选择最大的特征 $A_g$.
  4. 如果 $A_g$ 信息增益小于阈值, 则置 $T$ 为单节点树, 将 $D$ 中实例数最大的类 $C_k$ 作为该节点类标记, 返回 $T$.
  5. 否则对 $A_g$ 的每一可能值 $a_i$, 依 $A_g=a_i$ 将分割为 $D$ 若干子集 $D_i$, 作为 $D$ 的子节点.
  6. 对于 $D$ 的每个子节点 $D_i$, 如果 $D_i$ 为空, 则将 $D$ 中实例数最大的类作为标记, 构建子节点.
  7. 否则以 $D_i$ 为训练集, 以 $A-\{A_g\}$为特征集, 递归地调用得到子树 $T_i$, 返回 $T_i$.
  - 不足: 信息增益倾向于选择分枝比较多的属性.
  - 解决: 信息增益比. $A$ 为属性, $A$ 的不同取值将 $D$ 划分为 $n$ 个子集 $D_1$, $\cdots$, $D_n$.
    $g_R(D,A)=\dfrac{g(D,A)}{H_A(D)}.\\ H_A(D)=-\sum_{k=1}^{n}\dfrac{\vert D_k\vert}{\vert D\vert}\log_2\dfrac{\vert D_k\vert}{\vert D\vert}.$
- C4.5 算法:
  - 除了根据信息增益比选择特征外, C4.5 算法与 ID3 基本一样.
  - 增加了对连续值属性的处理, 对于连续值属性 A, 找到一个属性值 $a_0$, 将 $\le a_0$ 的划分到左子树, $＞a_0$ 的划分到右子树.
  - 不足: 信息增益比倾向于选择分割不均匀的特征, 轻重不均匀.
  - 解决: 先选择 n 个信息增益大的特征, 再从这 n 个特征中选择信息增益比最大的特征.
决策树学习——决策树的剪枝:
- 为防止出现过拟合, 对决策树进行简化的过程称为剪枝. 从已经生成的树上裁掉一些子树或者叶节点, 将其父节点作为新的叶节点, 用实例数最大的类别作为标记.
- 这种生成树再剪枝的方法称为后剪枝.
- 当数据量大时:
  - 将数据划分为训练集、验证集和测试集.
  - 用训练集训练得到决策树.
  - 从下向上逐步剪枝, 在验证集上测试性能, 直到性能下降为止.
  - 最后在测试集上的性能作为系统的性能.
- 当数据量小时:
  - 直接利用训练集进行剪枝.
  - 树 $T$ 的叶节点个数为 $\vert T\vert$, $t$ 是树 $T$ 的叶节点, 该节点有 $N_t$ 个样本, 其中 $k$ 类的样本点有 $N_{tk}$ 个 ($k=1,\cdots,K$). $H_t(T)$ 为叶节点 $t$ 上的经验熵, $a\ge 0$ 为参数.
    $C_a(T)=\sum_{t=1}^{\vert T\vert}N_tH_t(T)+a\vert T\vert.\\ C(T)=\sum_{t=1}^{\vert T\vert}N_tH_t(T)=-\sum_{t=1}^{\vert T\vert}\sum_{k=1}^{K}N_{tk}\log\dfrac{N_{tk}}{N_t}.$
    其中 $C(T)$ 表示对训练数据的预测误差, $\vert T\vert$ 表示模型的复杂程度.
- 剪枝就是当 $a$ 确定时, 选择损失函数最小的模型.
  - 输入: 生成算法产生的整个树 $T$, 参数 $a$.
  - 输出: 修剪后的子树 $T_a$.
  1. 计算每个节点的经验熵.
  2. 递归地从树的叶节点向上回缩, 如果回缩后的损失函数小于等于回缩前, 则剪枝将父节点变为新的叶节点.
  3. 返回 2, 直至不能继续为止, 得到损失函数最小的子树 $T_a$.
随机森林:
- 决策树容易过拟合.
- 随机森林是由多个决策树组成的分类器.
- 通过投票机制改善决策树.
- 单个决策树的生成:
  - 有放回的数据采样.
  - 属性 (特征) 的采样.
- 集外数据的使用:
  - 单个决策树未用到的数据.