人工智能导论 笔记2

第二章 神经网络和深度学习

神经网络 —— 从数字识别说起

• 深度学习 $\subseteq$ 机器学习 $\subseteq$ 人工智能.

  

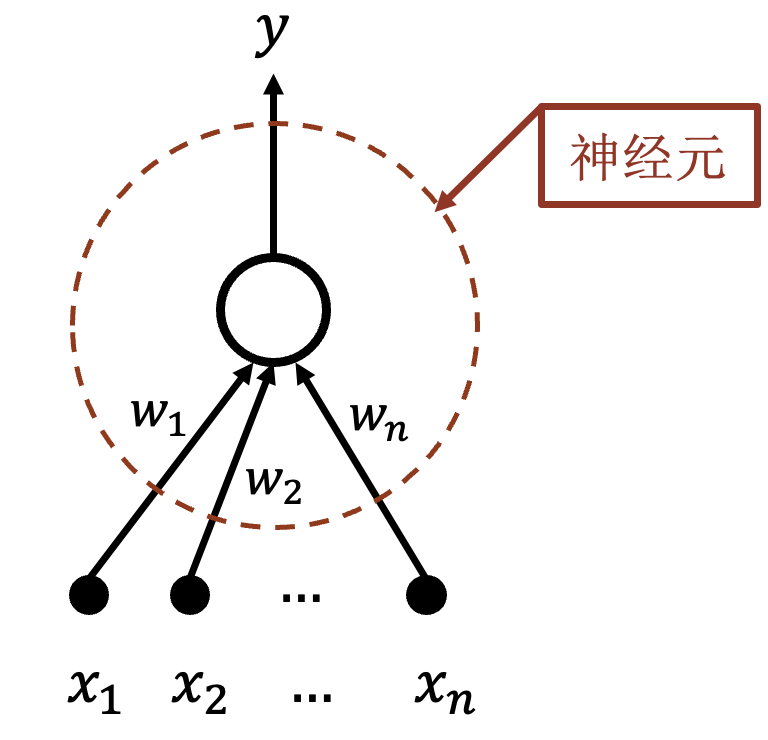
• $w_i(1\le i\le n)$ 表示数字模式, $x_i(1\le i\le n)$ 表示数字图像, 大小表示匹配程度.

  $$net=\sum_{i=1}^{n}w_i\cdot x_i.$$

• Sigmoid 函数: 评判匹配的程度, 将匹配结果变换到 0~1 之间.

  $$\sigma(net)=\dfrac{1}{1+e^{-net}}.$$

• 增加偏置项: 使 Sigmoid 函数平移.

  $$net=\sum_{i=1}^{n}w_i\cdot x_i+b;\\ y=sigmoid(net).$$

  

  

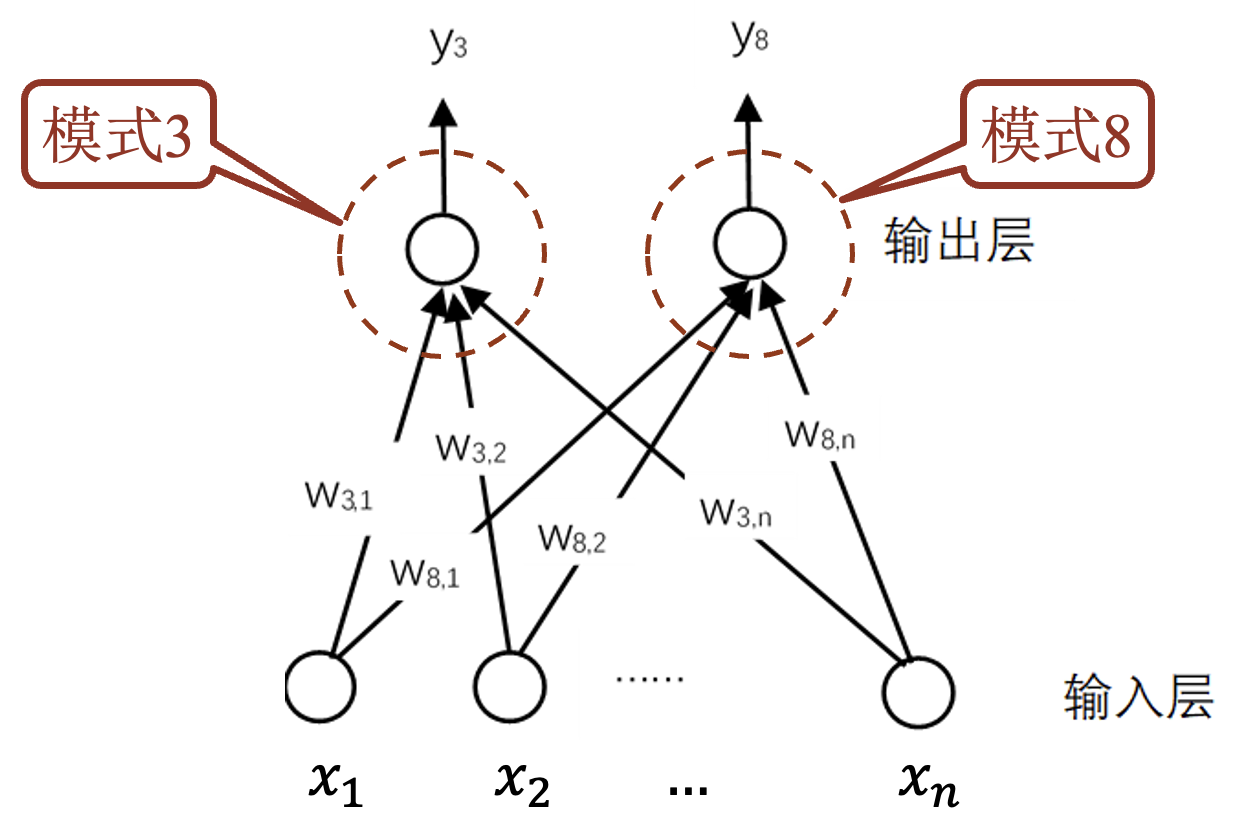
• 神经元代表一个模式, 其输出为匹配结果.

• 神经网络的扩展:

  • 横向 —— 增加模式.

    

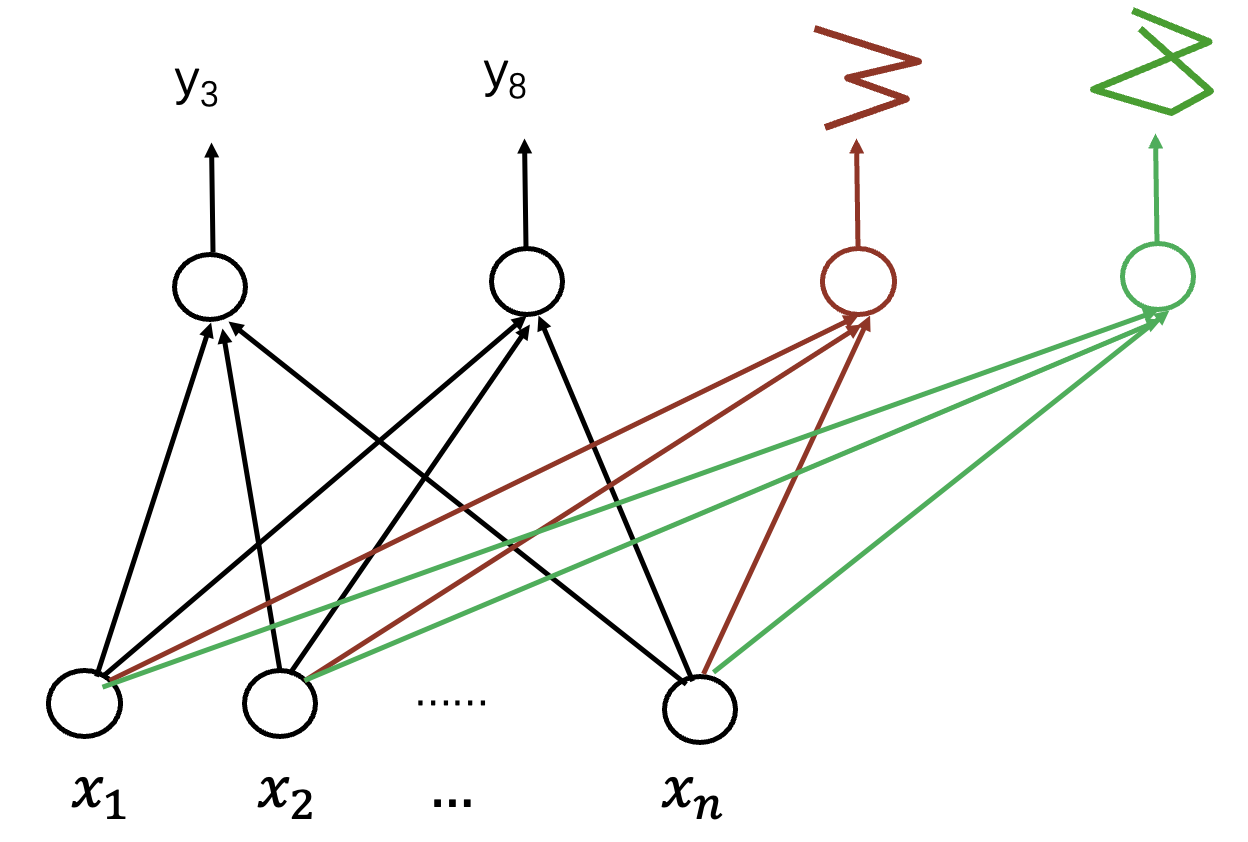
  • 纵向 —— 局部模式.

    

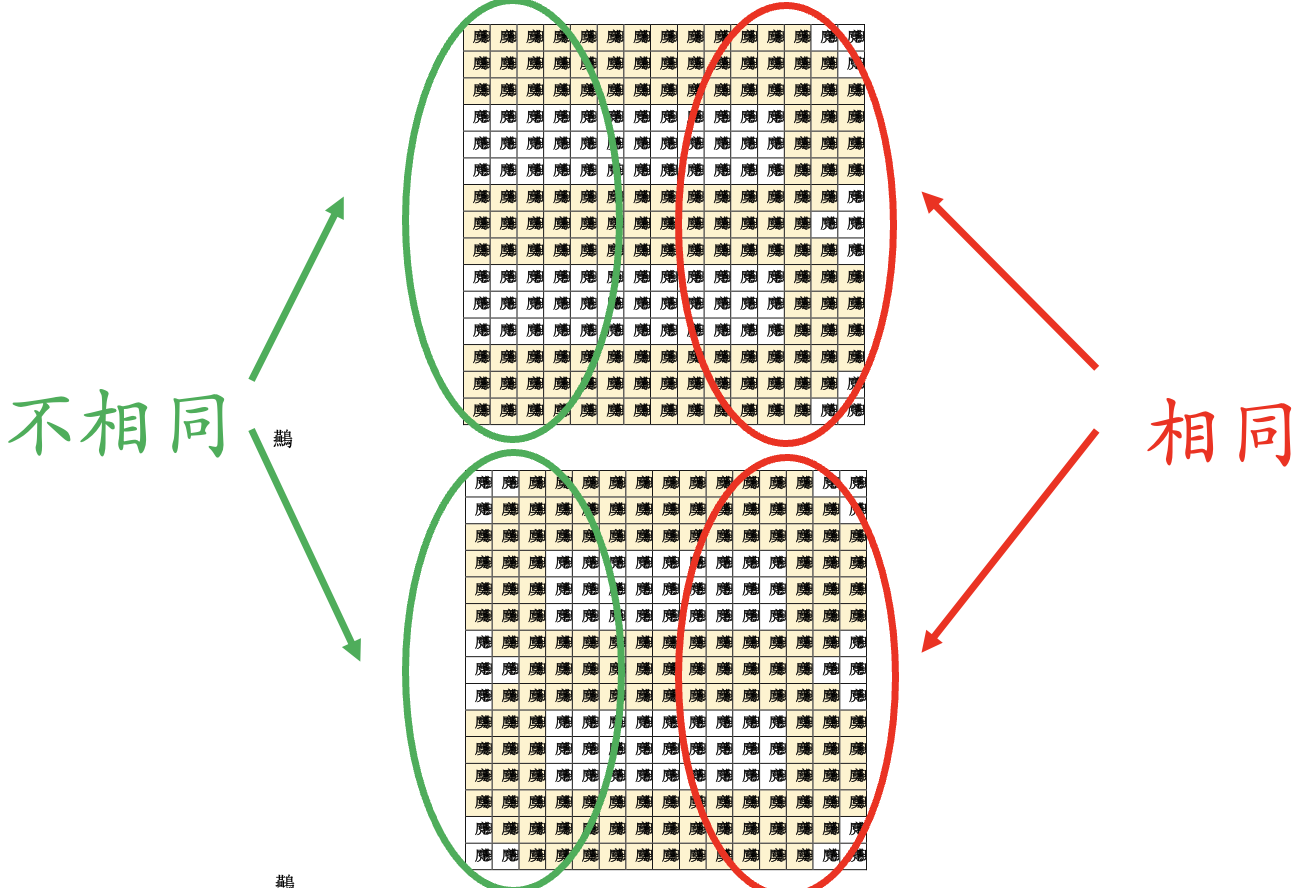
  • 网络更深 —— 模式组合.

    

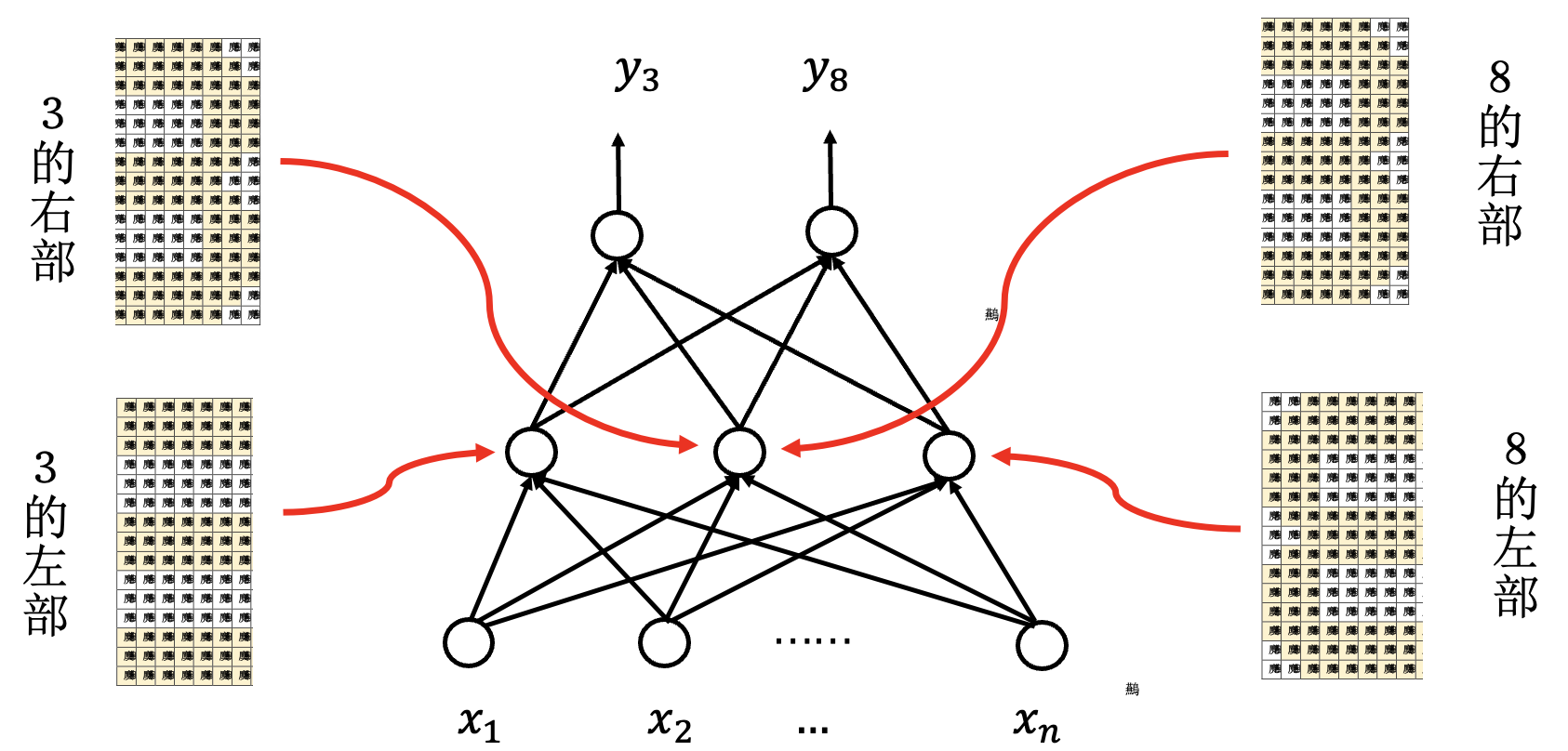
• 获得模式:

  • 模式通过神经元的连接权重表示.
  • 通过训练样本, 自动学习权重 (模式), 不是人工设计.
  • 学习到的模式是一种隐含表达.

神经元与神经网络

• 神经元:

  $$net=\sum_{i=1}^{n}w_i\cdot x_i+b=\sum_{i=0}^{n}w_i\cdot x_i;\\ o=g(net).$$

  

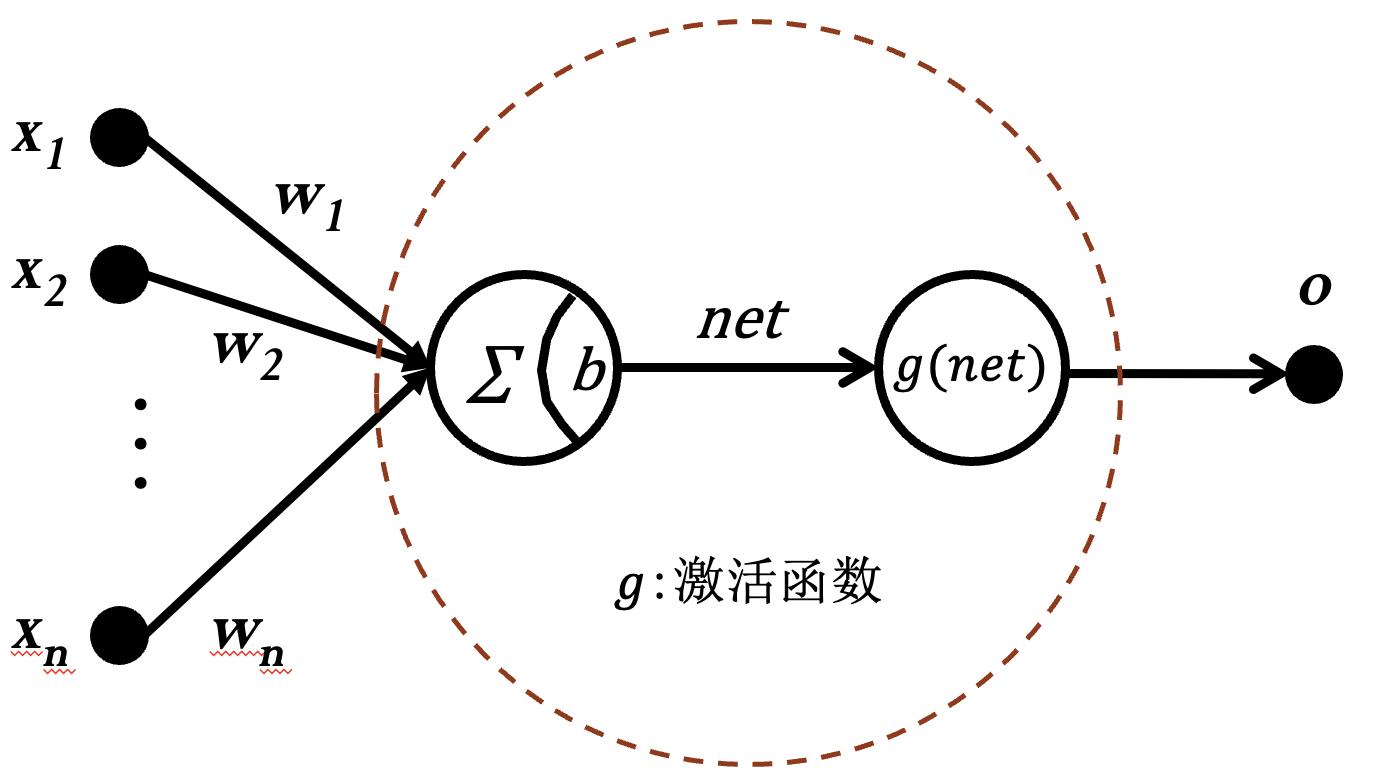
• 激活函数:

  • 符号函数.

  • Sigmoid 函数.

  • 双曲正切函数.

  • ReLU 函数.

  • Softmax 函数.

    $$o_k=\dfrac{e^{net_k}}{\sum\limits_{i=1}^{m}e^{net_i}}.$$

    

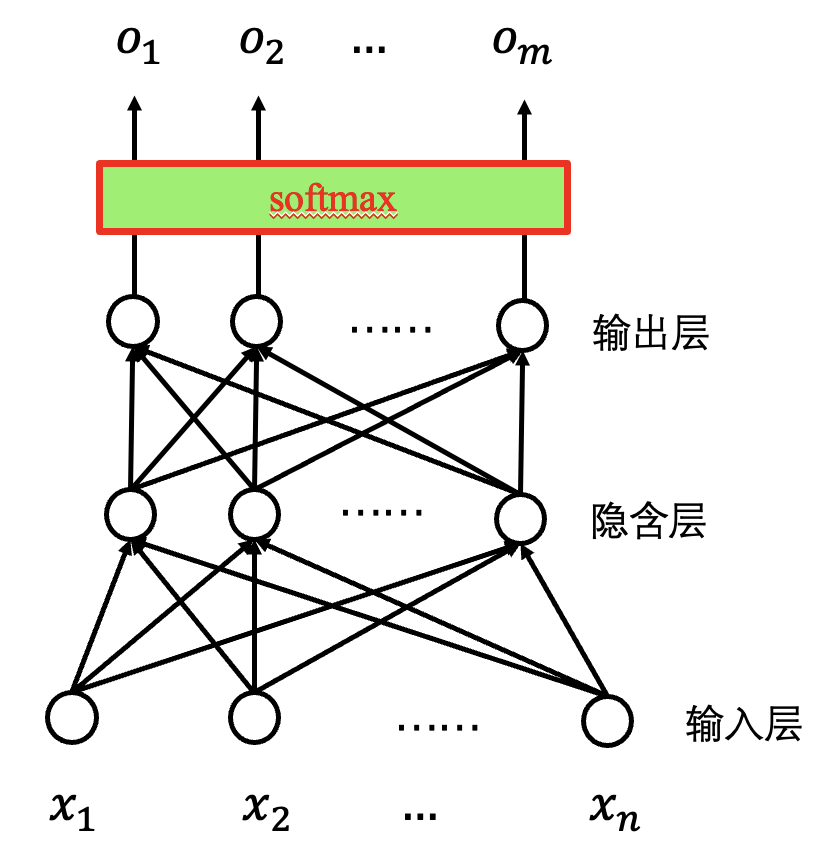
如何训练神经网络

• 建立数据集 (以动物识别为例):

  • 收集各种动物的照片:
    • 不同姿势.
    • 不同角度.
    • 不同大小.
  • 数据标注:
    • 每张照片标注上动物的名称.
  • 训练集与测试集:
    • 样本.

• 训练网络: 调整神经元权重.

• 评价效果: 损失函数.

• 误差平方和损失函数:

  • 用于输出是具体数值的问题.

  • 对样本 $d$ 的误差:

    $$E_d(w)=\dfrac{1}{2}\sum_{k=1}^{m}(t_{kd}-o_{kd})^2.$$

  • 对所有样本的误差:

    $$E(w)=\sum_{d=1}^{n}E_d(w)=\dfrac{1}{2}\sum_{d=1}^{n}\sum_{k=1}^{m}(t_{kd}-o_{kd})^2.$$

    

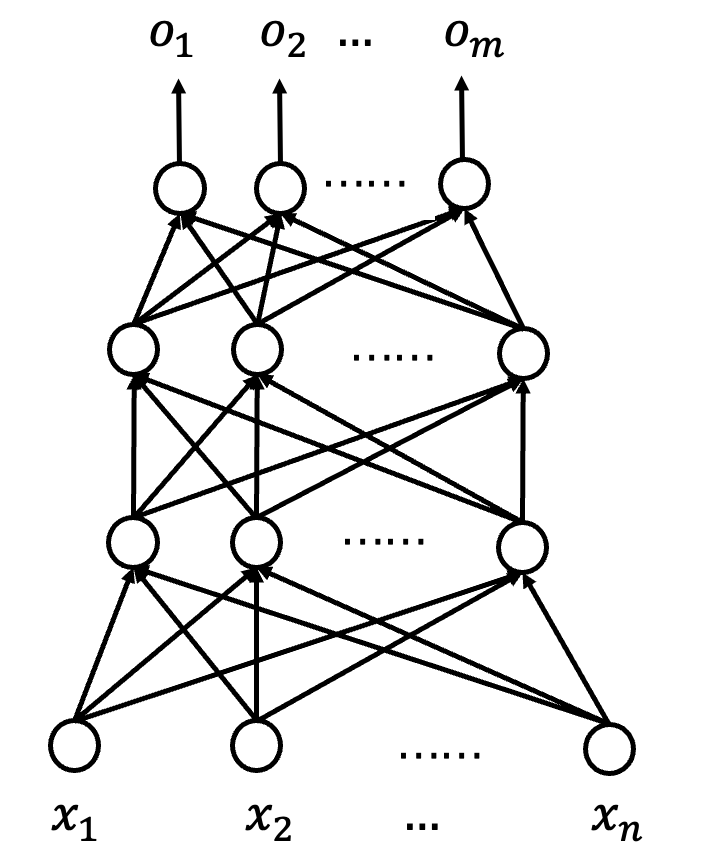
• 梯度下降法:

  • 迭代公式: 对权重求导, 作为下降的梯度大小.

    $$w_i^{new}=w_i^{old}+\Delta w_i,\,\Delta w_i=-\eta\dfrac{\part E(w)}{\part w_i}.\\ \Rightarrow w^{new}=w^{old}+\Delta w,\,\Delta w=-\eta\nabla_wE(w)=-\eta\big[\dfrac{\part E(w)}{\part w_i}\big]_{1\le i\le n}.$$

  • 梯度下降算法:

    • 批量梯度下降算法.
    • 随机梯度下降算法.
    • 小批量梯度下降算法.

    

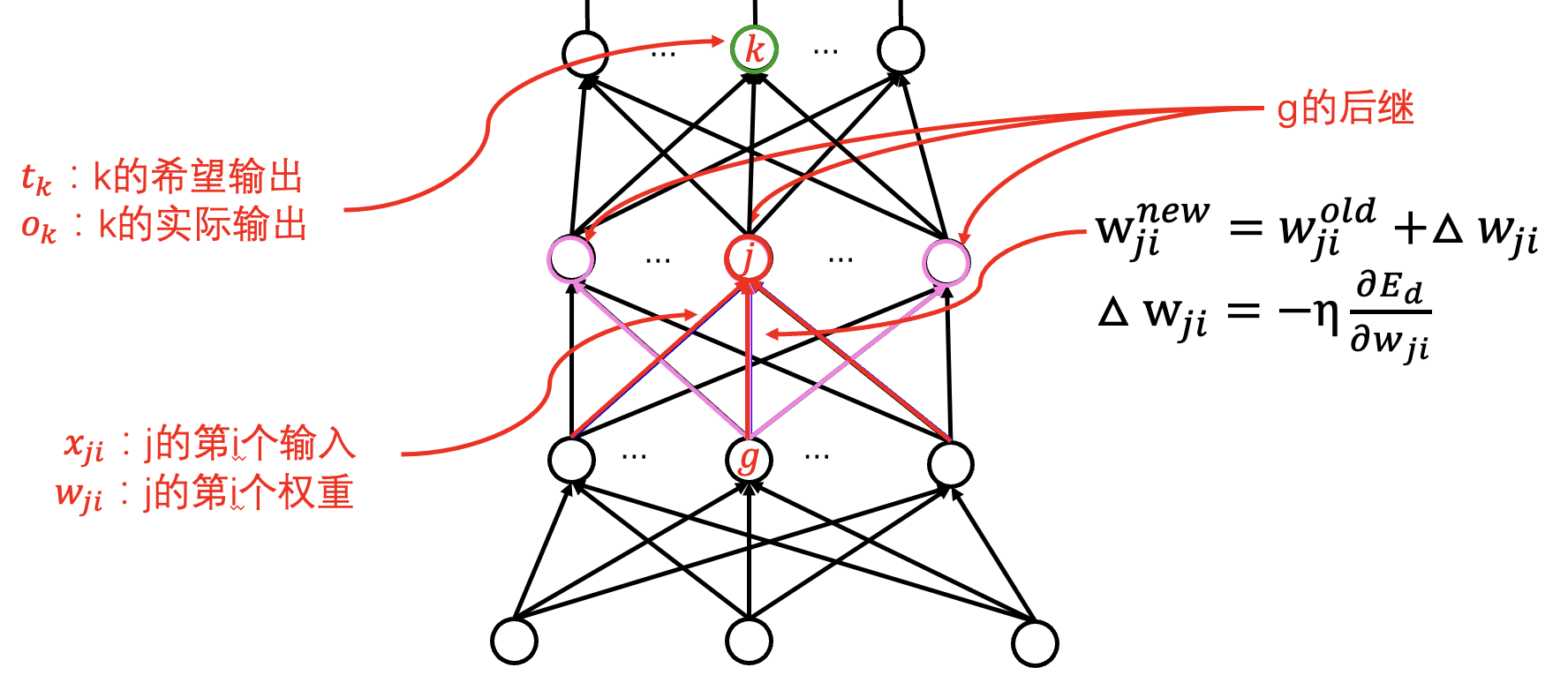
  • 输出层 (只影响一个输出):

    

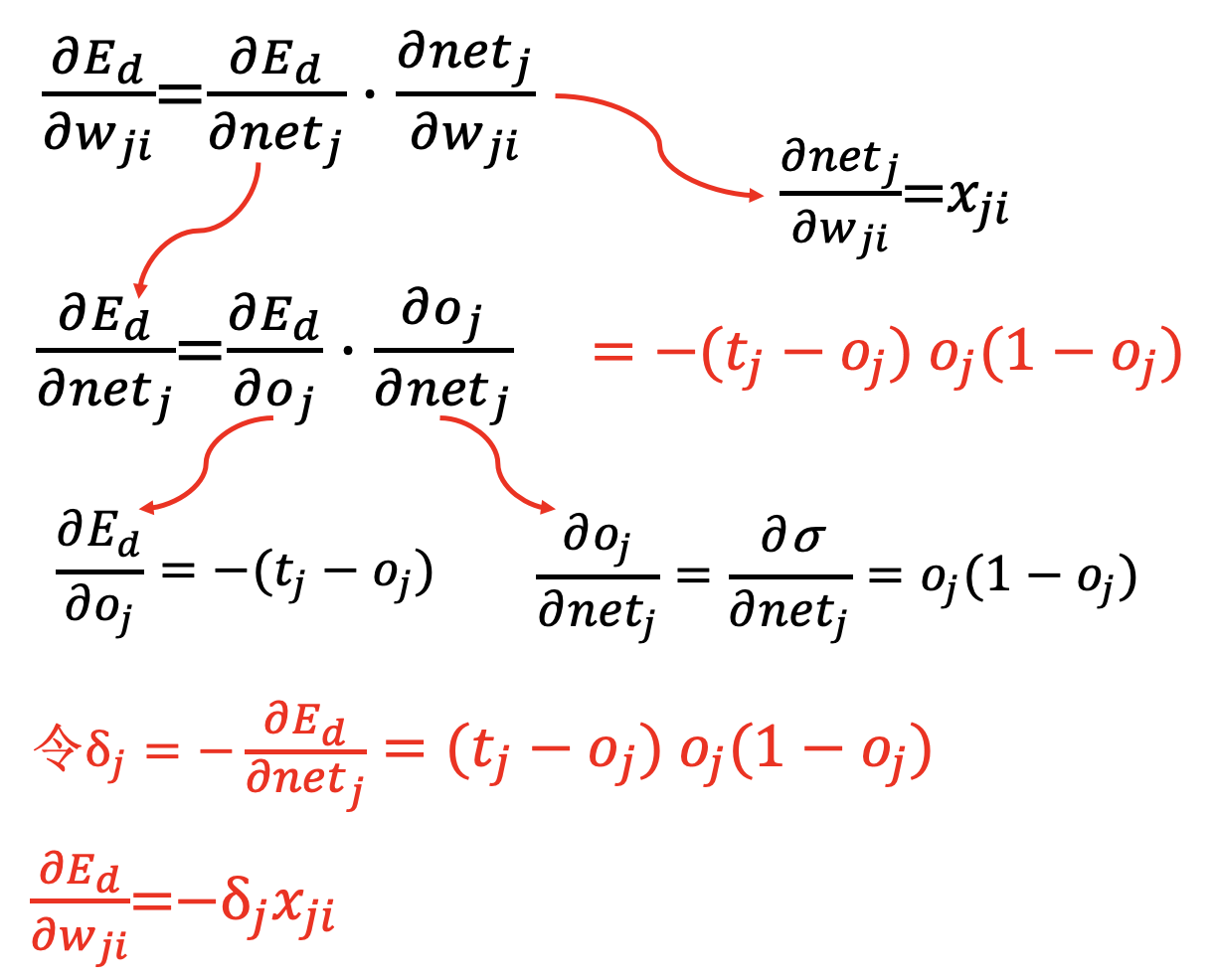
  • 隐含层 (影响多个输出):

    

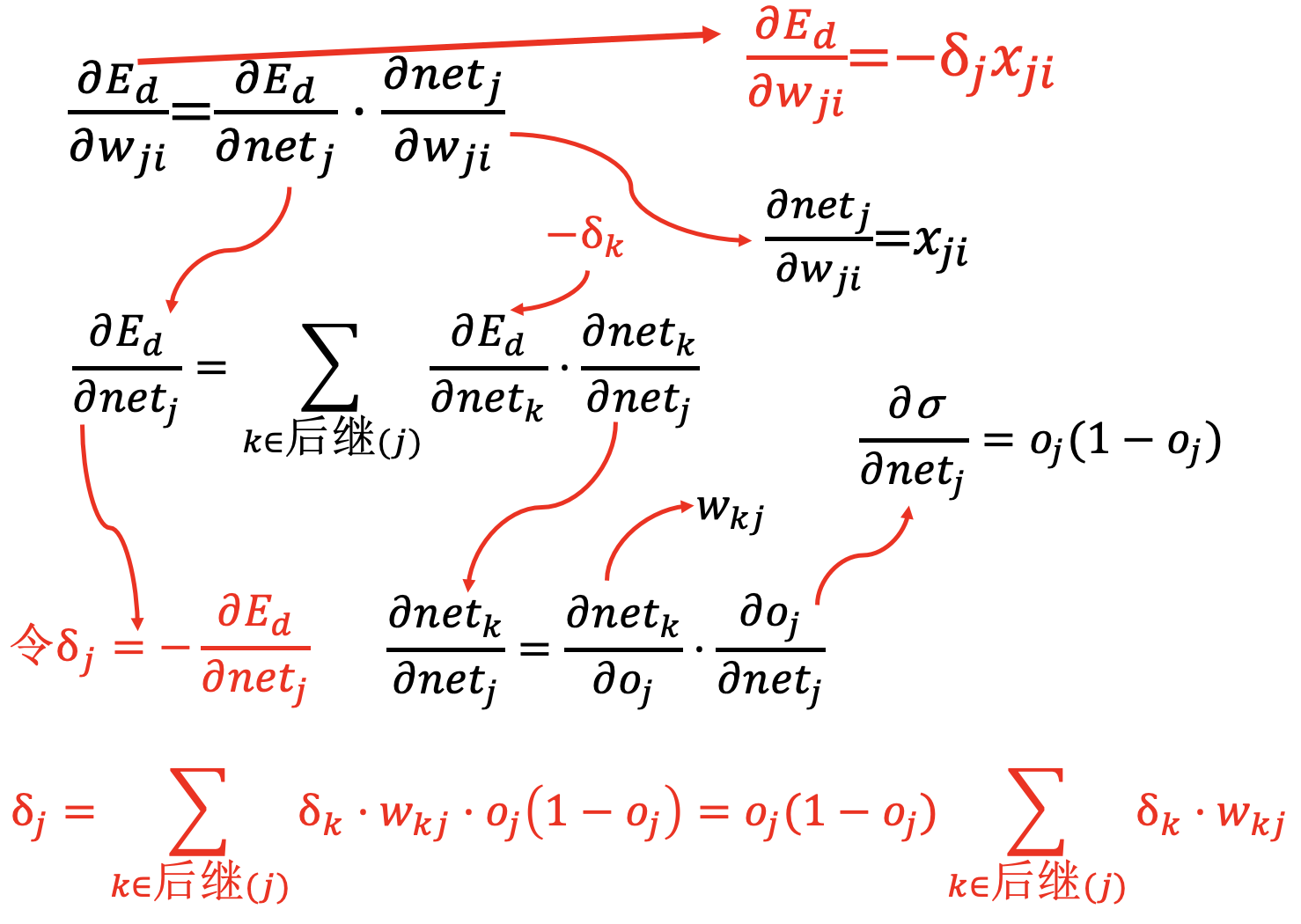
  • 整体梯度计算:

    

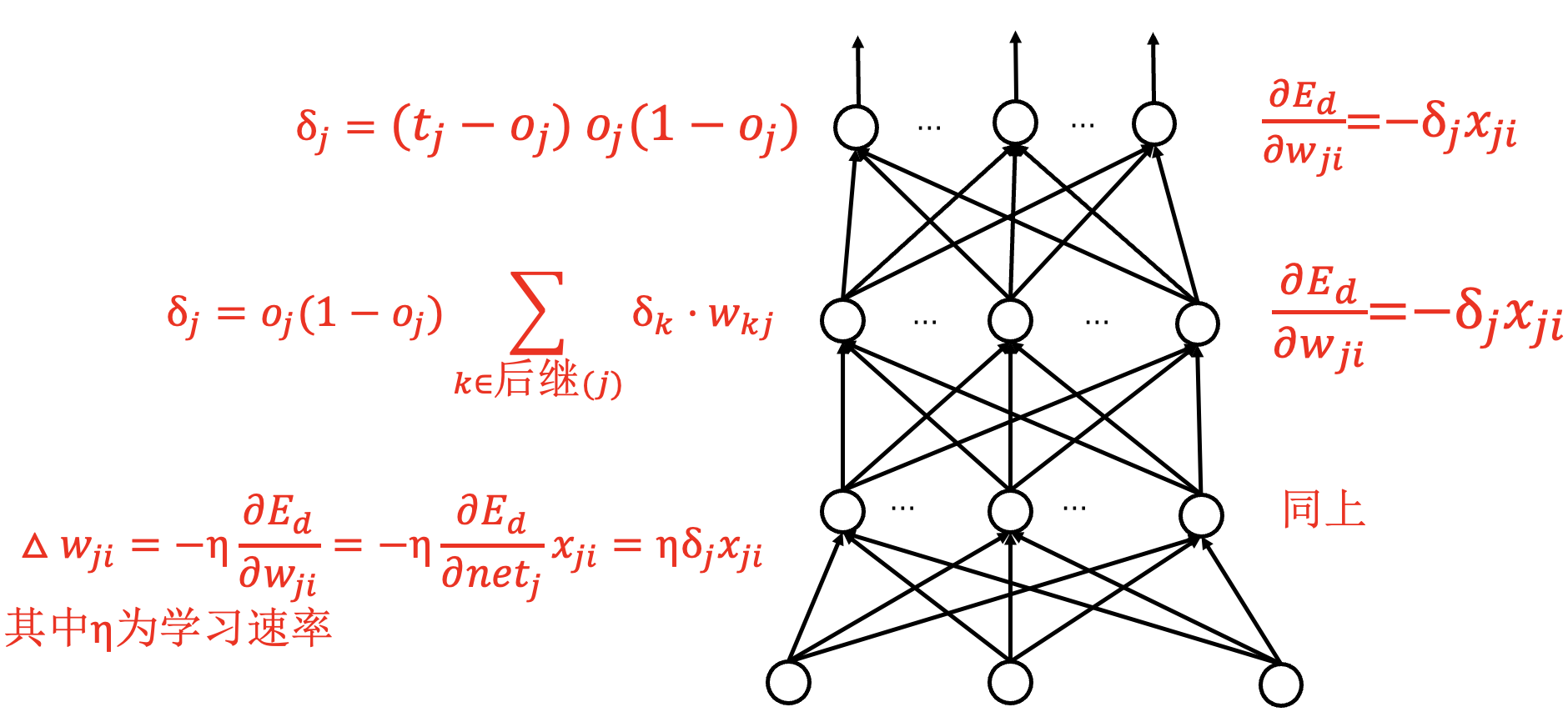
• 反向传播算法 (BP算法): 随机梯度下降算法的一种实现.

  

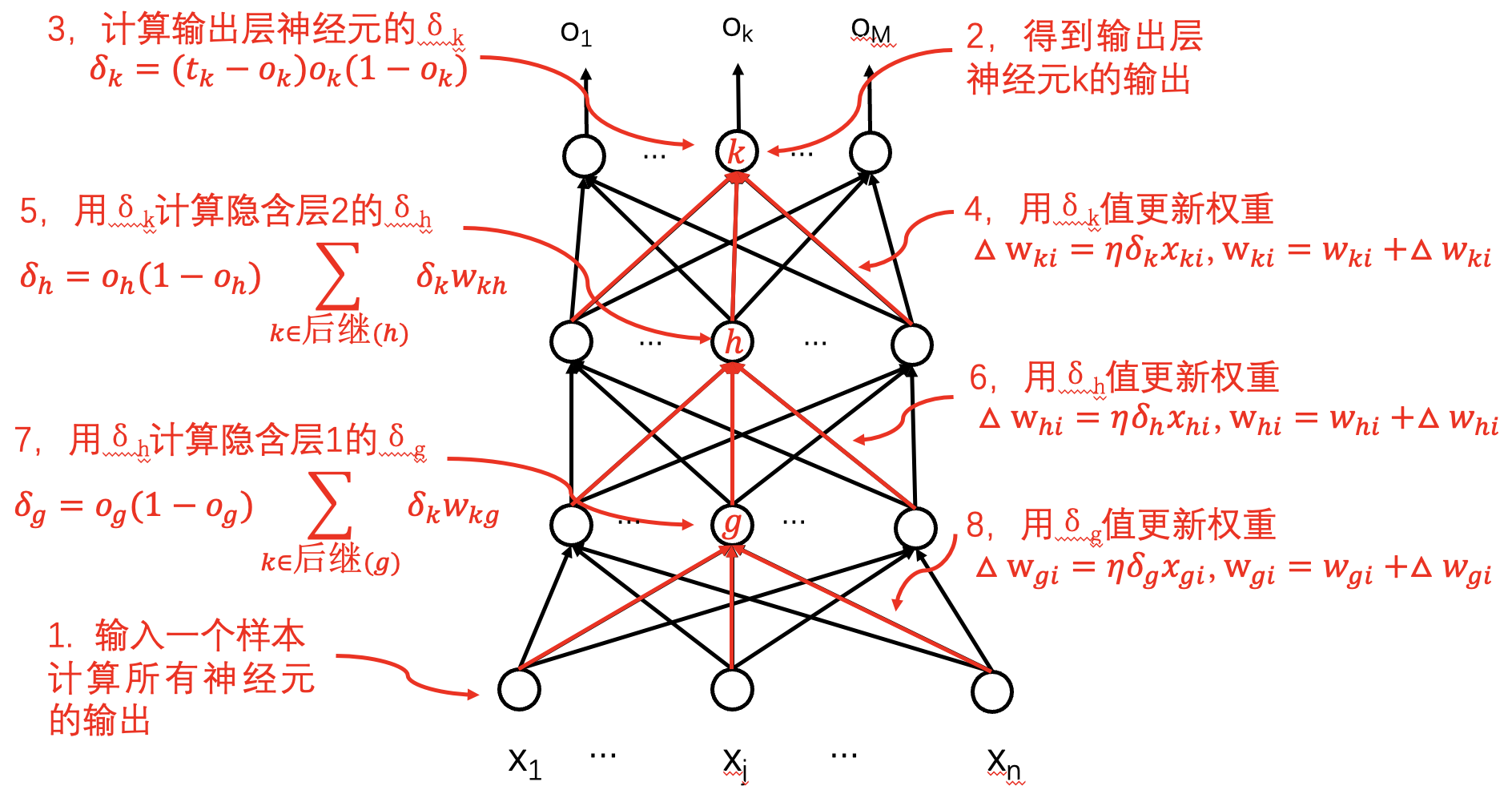
  • 随机梯度下降版: 初始化所有权值为小的随机值, 如 $[-0.05,0.05]$.
  • 算法条件:
    • 全连接网络.
    • 批量、小批量梯度下降算法.
    • 激活函数: Sigmoid 函数.
    • 损失函数: 误差平方和.

• 交叉熵损失函数:

  $$H_d(w)=-\sum_{k=1}^{M}t_{kd}\log o_{kd}.\\ H(w)=\sum_{d=1}^{N}H_d(w)=-\sum_{d=1}^{N}\sum_{k=1}^{M}t_{kd}\log o_{kd}.$$

  其中 $t_{kd}$ 为样本的希望输出值, $o_{kd}$ 为样本的实际输出值, 需要为概率值. 这给出了两个不同的概率分布间的距离. 对于分类问题, 对于给定输入样本 $d$, 只有 $d$ 对应的希望输出为 1, 其他为 0. 此时

  $$H_d(w)=-\log o_{kd}.\\$$

  

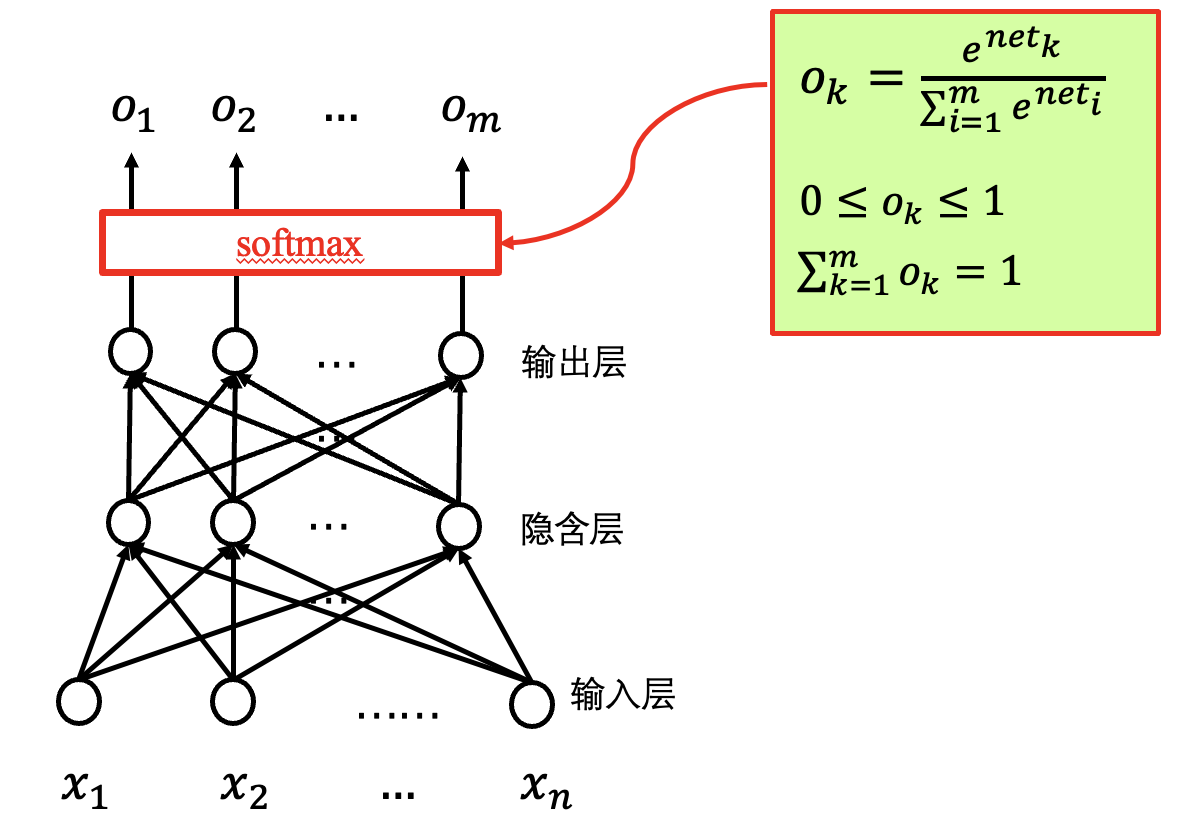
卷积神经网络 (CNN)

• 全连接网络的不足:

  • 连接权重过多.
  • 影响训练速度.
  • 影响使用速度.

• 卷积神经网络的特点:

  • 参数少, 只与卷积核的大小和数量有关.
  • 具有特征抽取能力.
  • 特征的平移不变性 (一定程度上).

• 提取局部模式:

  

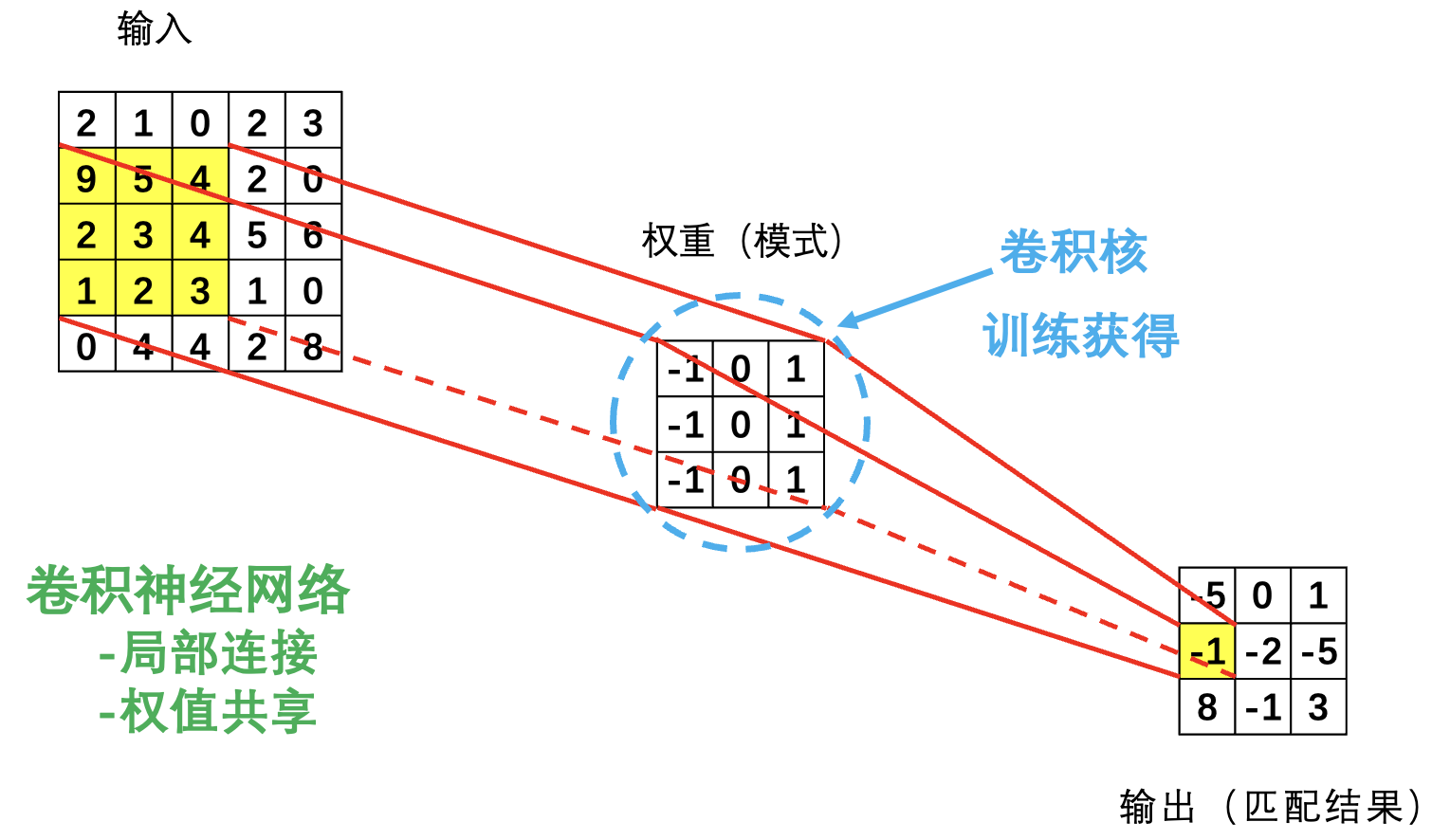
  • 局部连接, 权值共享.

  • 卷积核训练通过 BP 算法进行.

  • 多卷积核: 一个卷积核产生一个通道, 输出的通道数等于卷积核数.

  • 多输入通道 (例: RGB 识别):

    

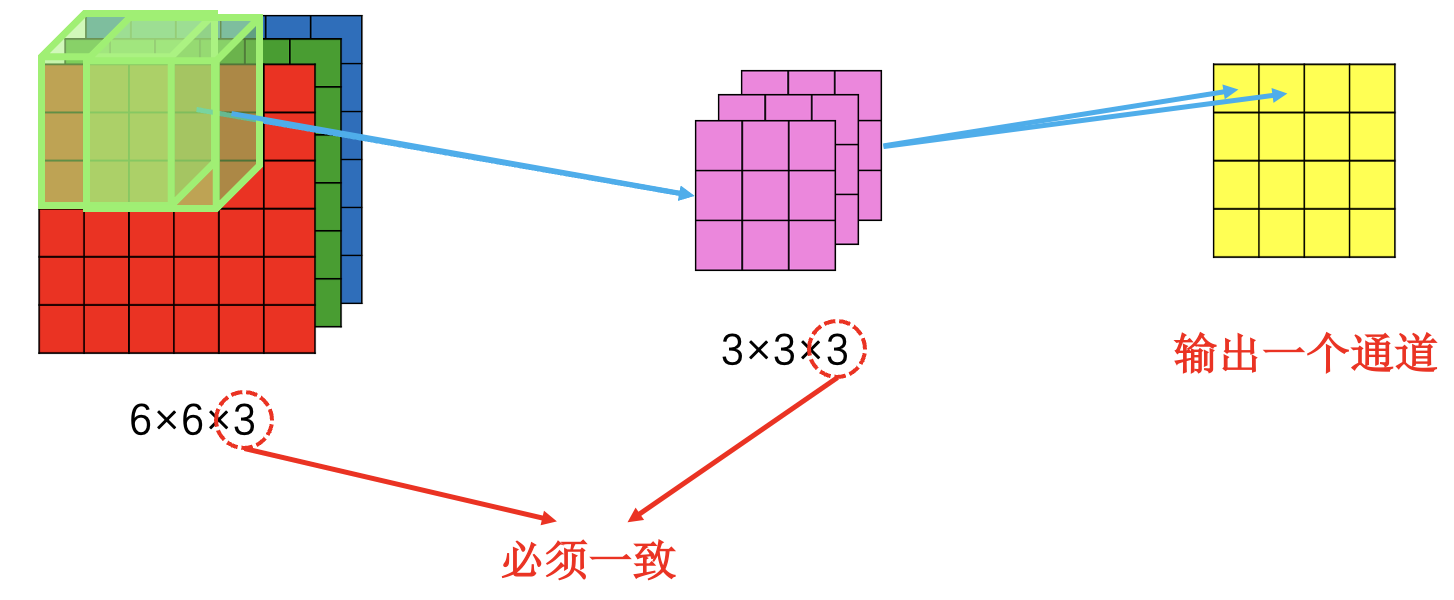
    此时视为多厚度单卷积核.

  • 卷积核大小: 多层小卷积实现大卷积 (两层 3×3 卷积等效 5×5 卷积).

  • 池化: 一种降维的手段 (最大池化/平均池化), 池化不改变通道数.

  • 卷积核具有抽取特征的能力.

• LeNet 神经网络 (数字识别):

  

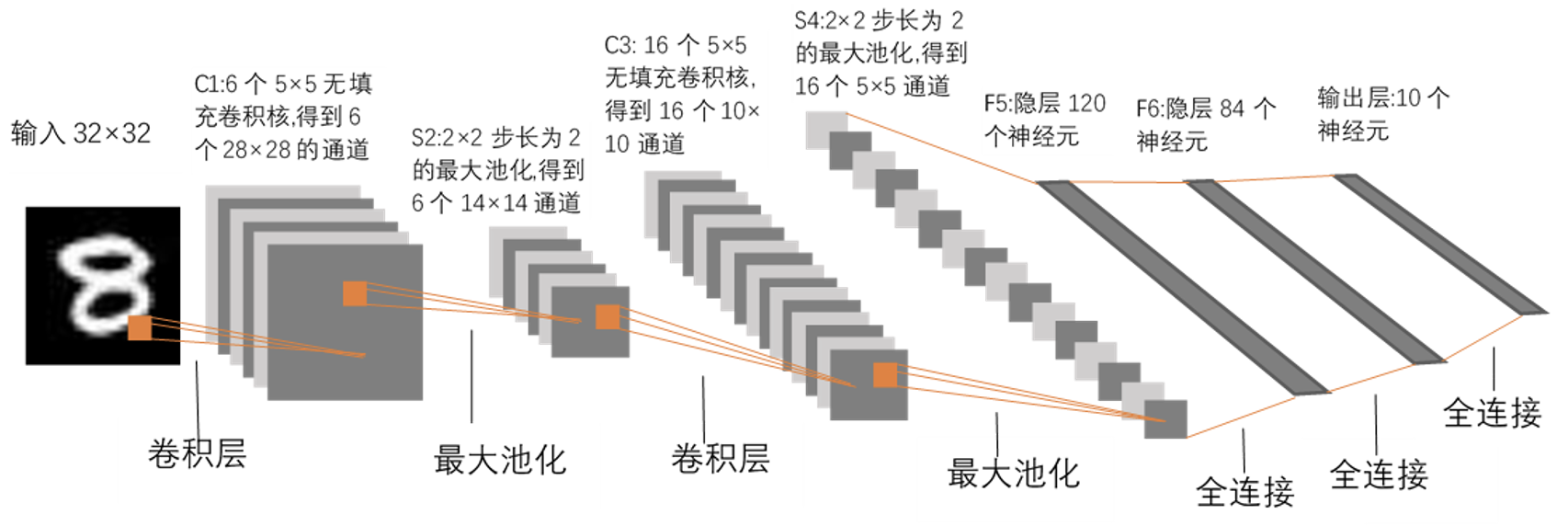
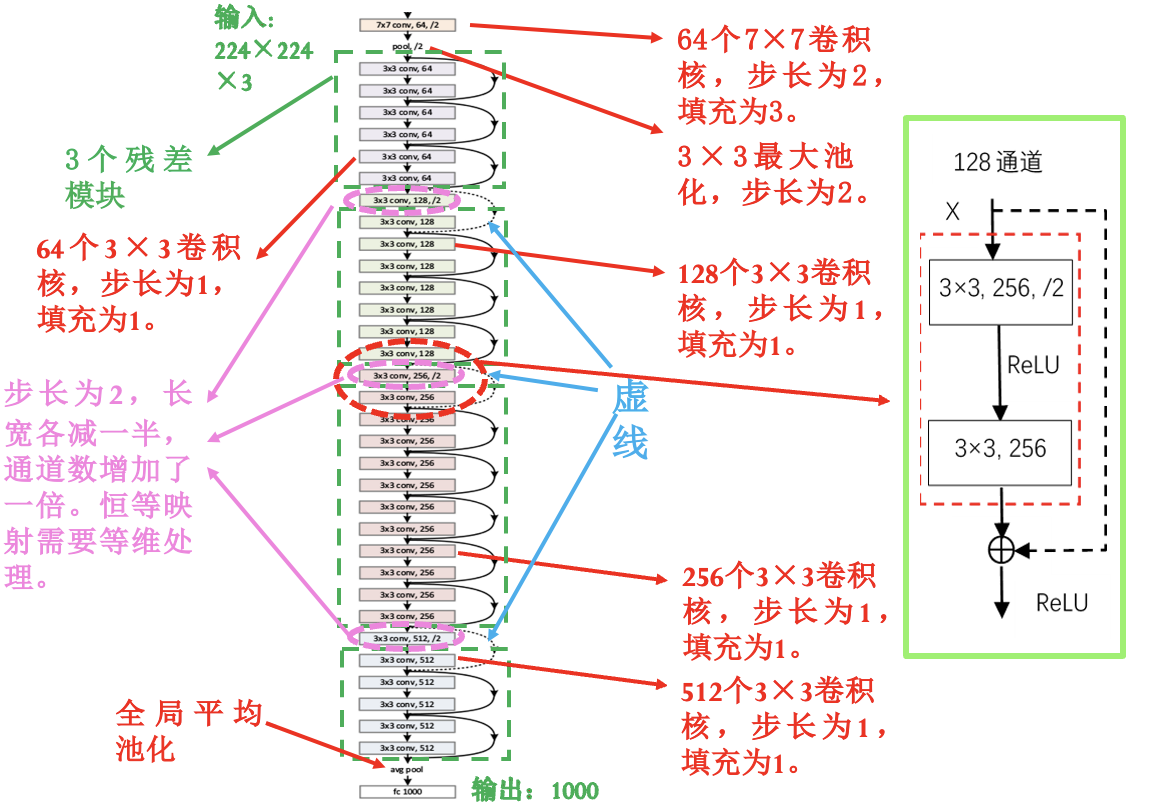
• VGG-16 神经网络 (图像识别):

  

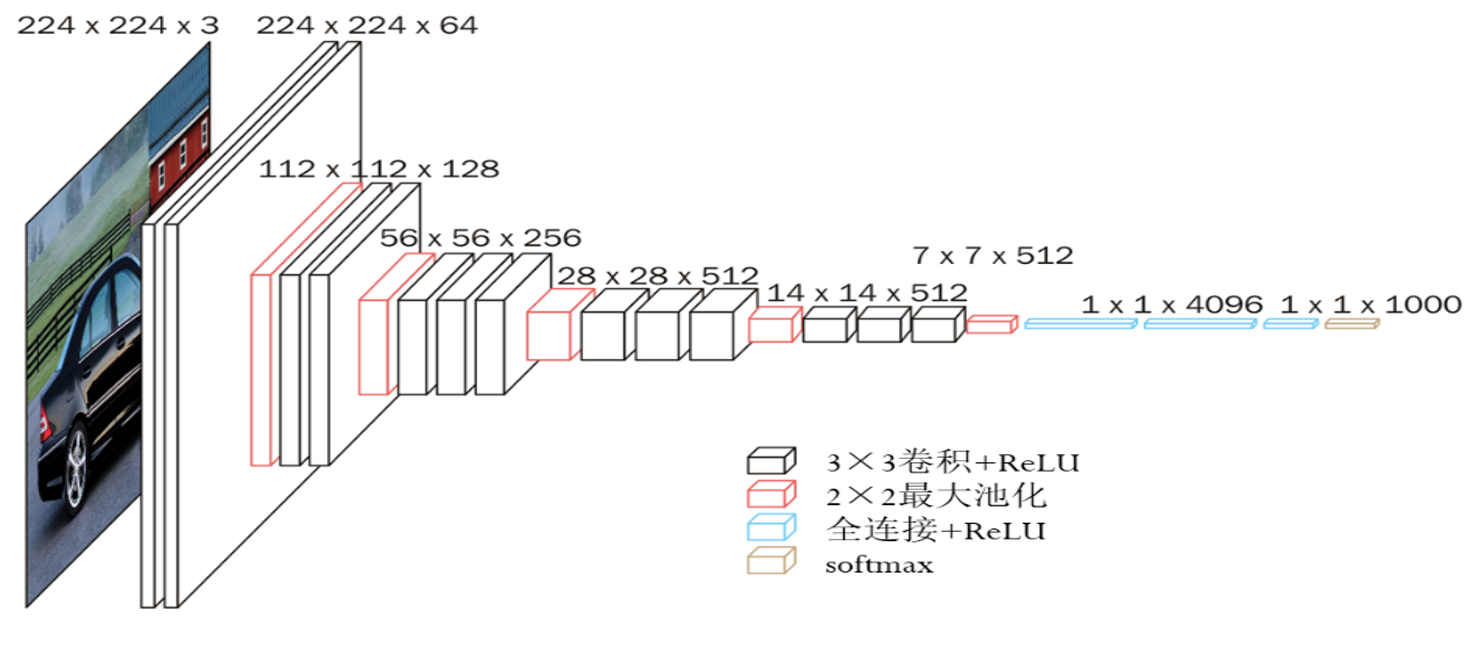
梯度消失问题

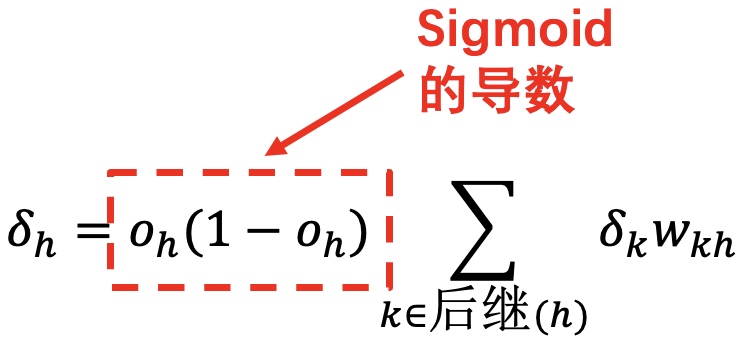
• 网络深度过深时:

  

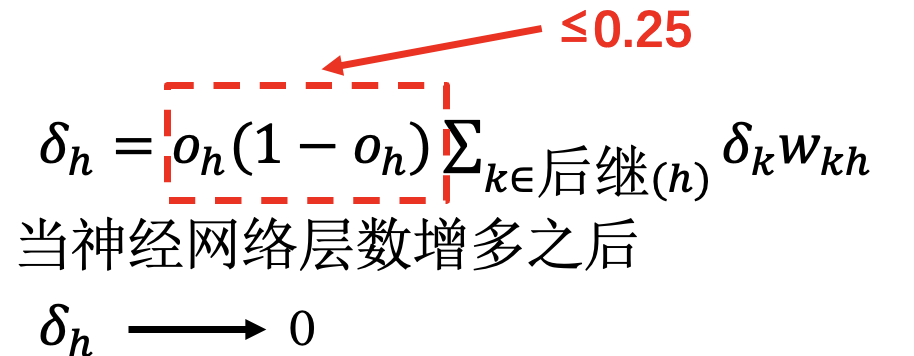
• 使用 ReLU 激活函数, 其导数恒为 1:

  

• GoogLeNet 神经网络 (类比高楼供水系统):

  

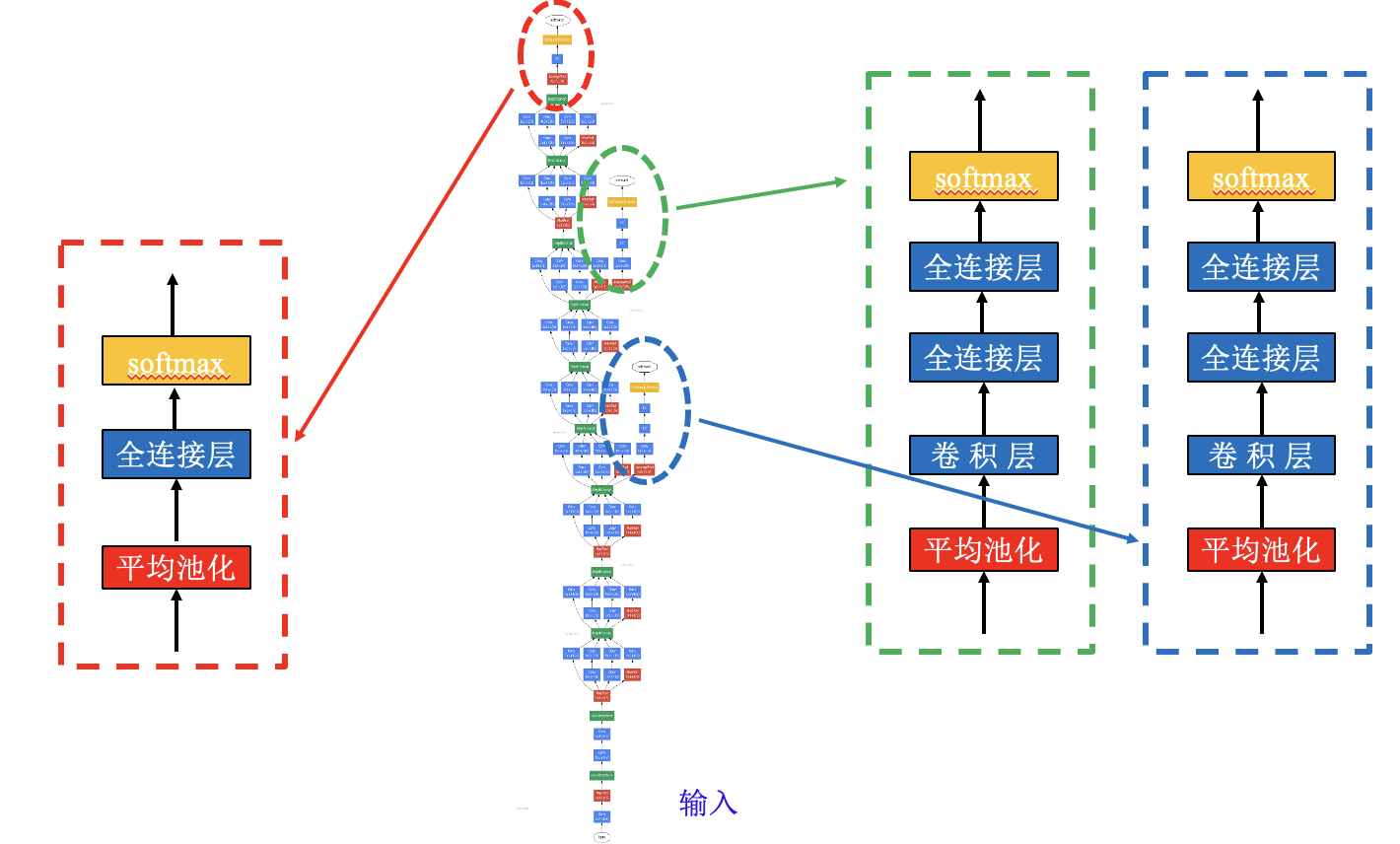
  神经元依靠就近输出进行训练时的梯度计算补偿, 训练结束后只采用最终输出.

  • Inception 模块:

    

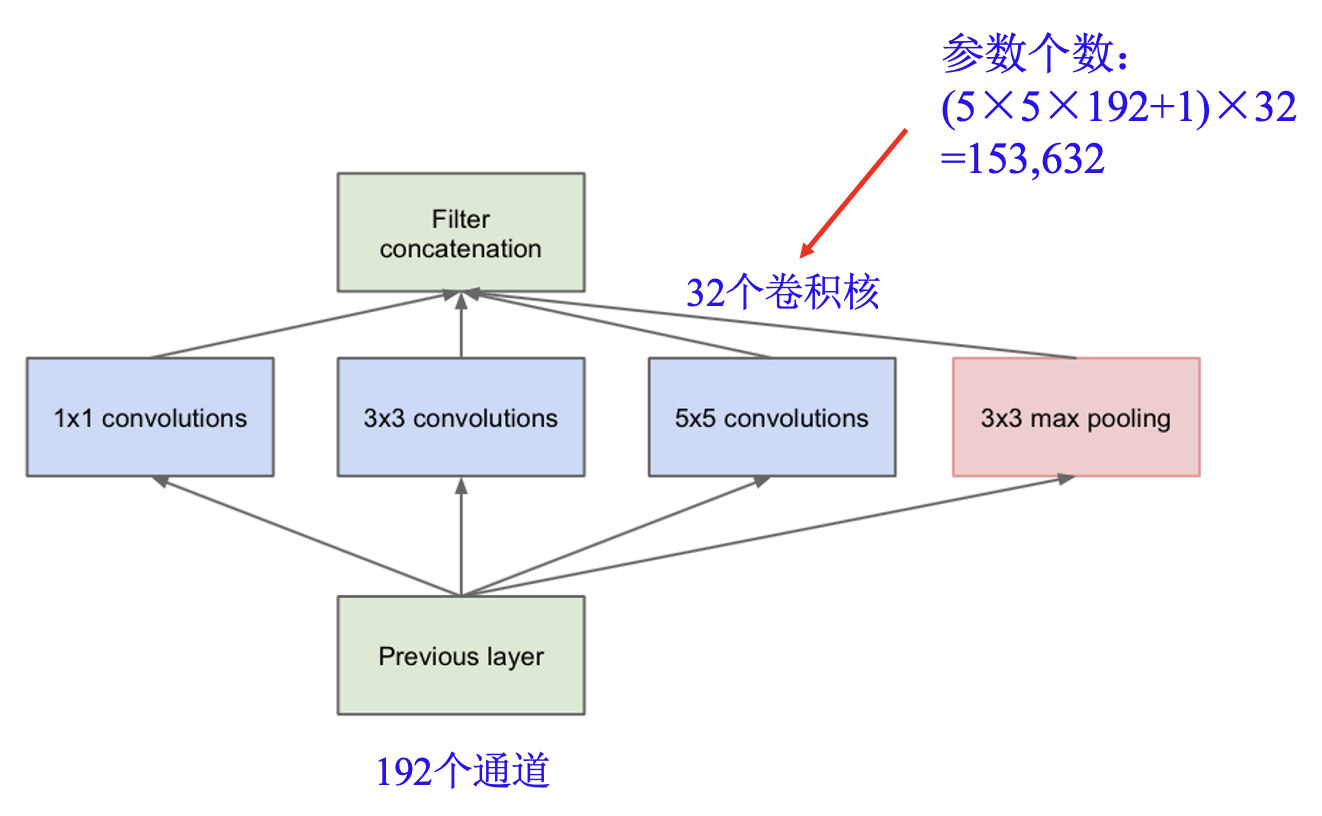
    —同时使用不同大小的卷积核.

  • 降维 Inception 模块:

    

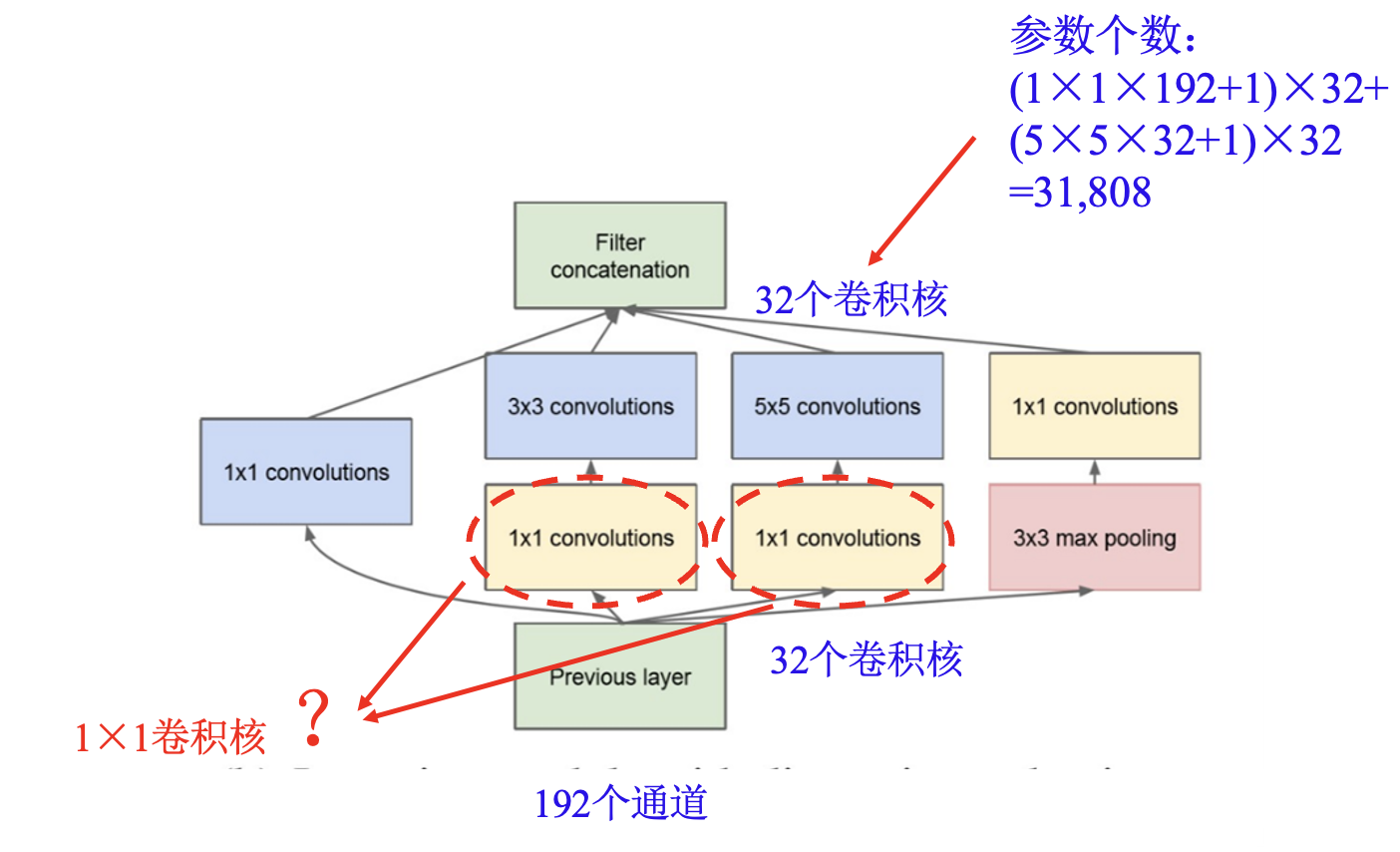
    使用 1×1 卷积降维.

  • Inception 模块详析:

    

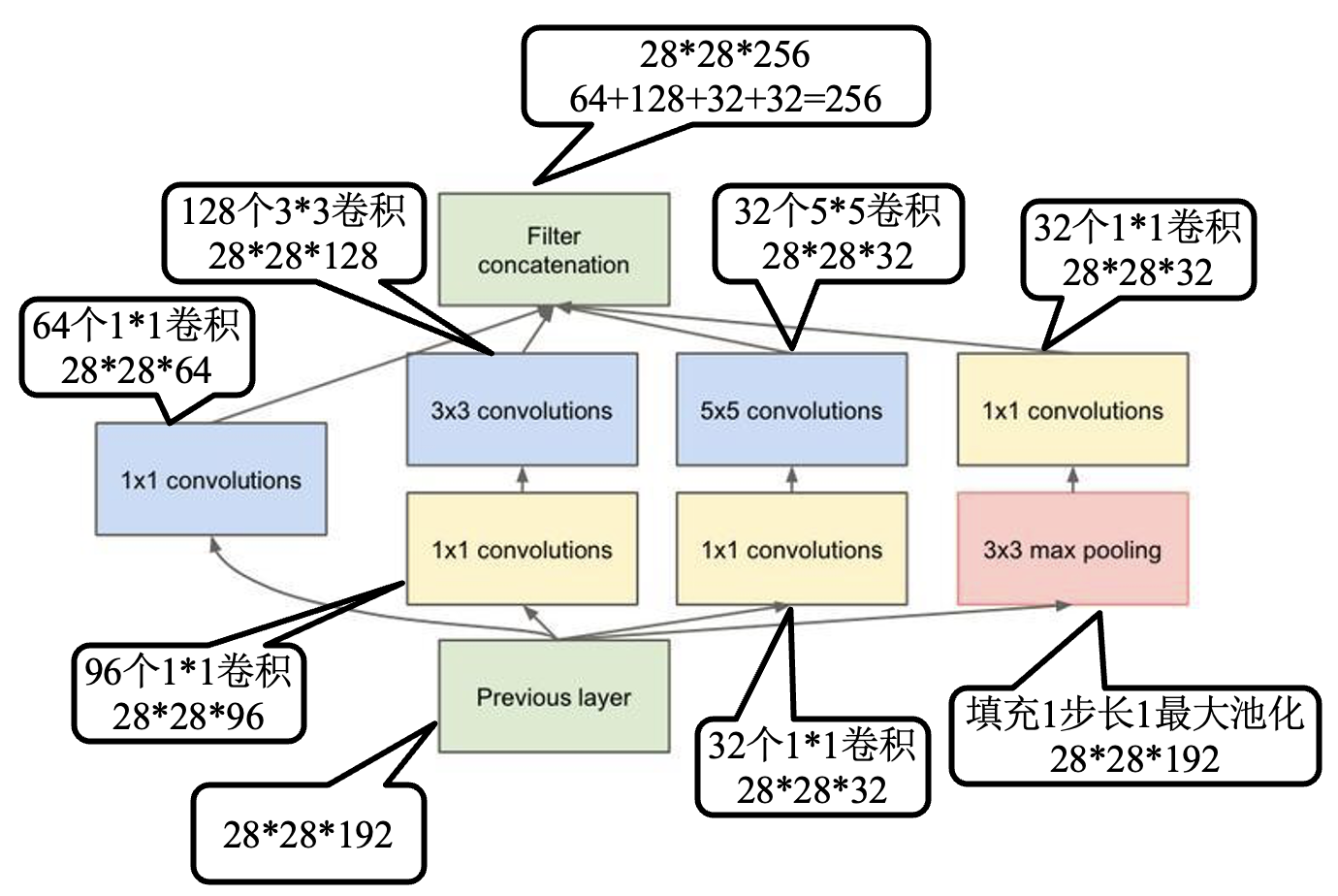
• ResNet 残差网络:

  • 神经网络的退化现象 (与网络结构有关):

    

    

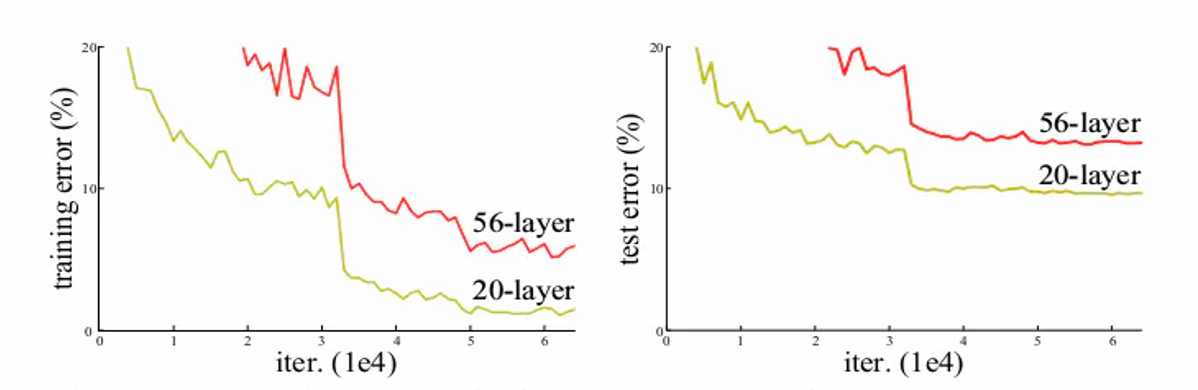
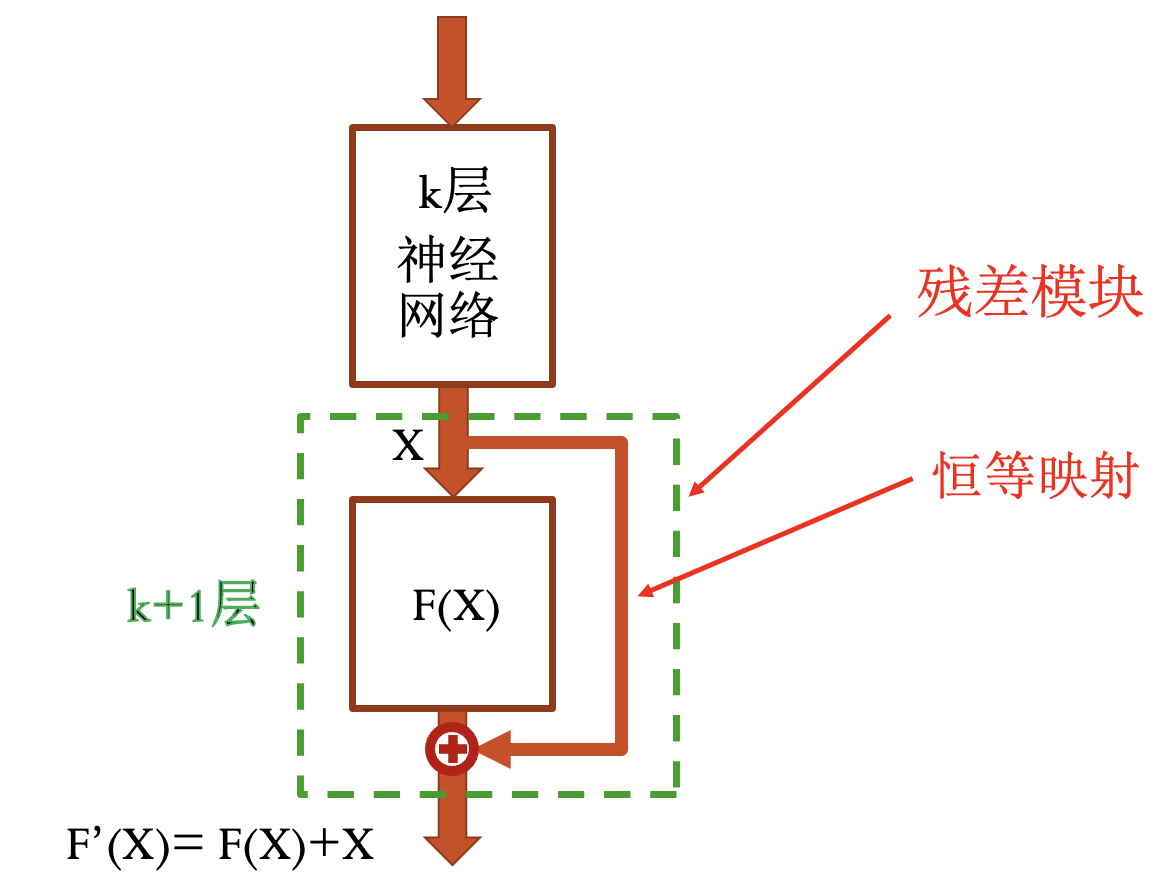
  • 残差模块:

    

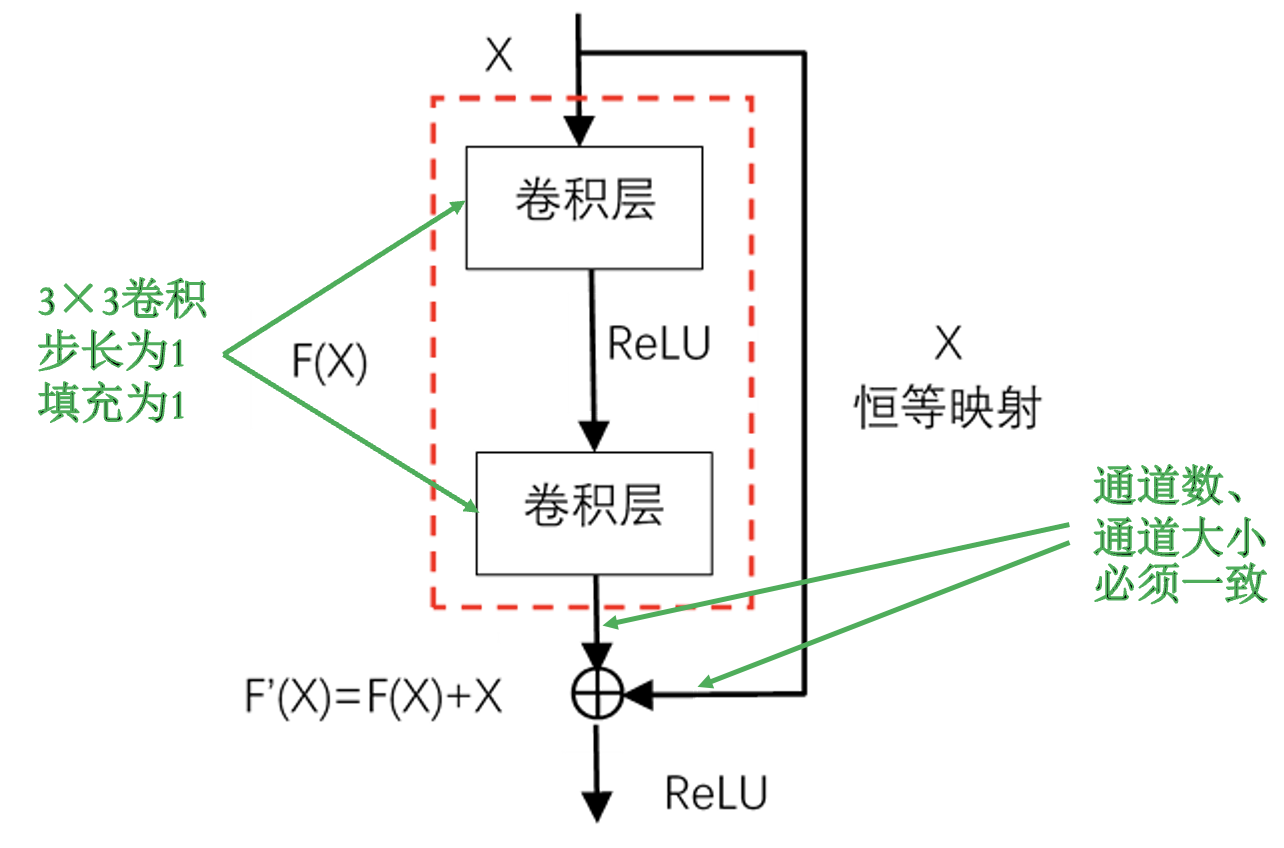
    恒等映射的存在解决了梯度消失问题.

    

过拟合问题

• 神经网络的过拟合问题 (与网络结构无关, 与训练轮次有关):

  

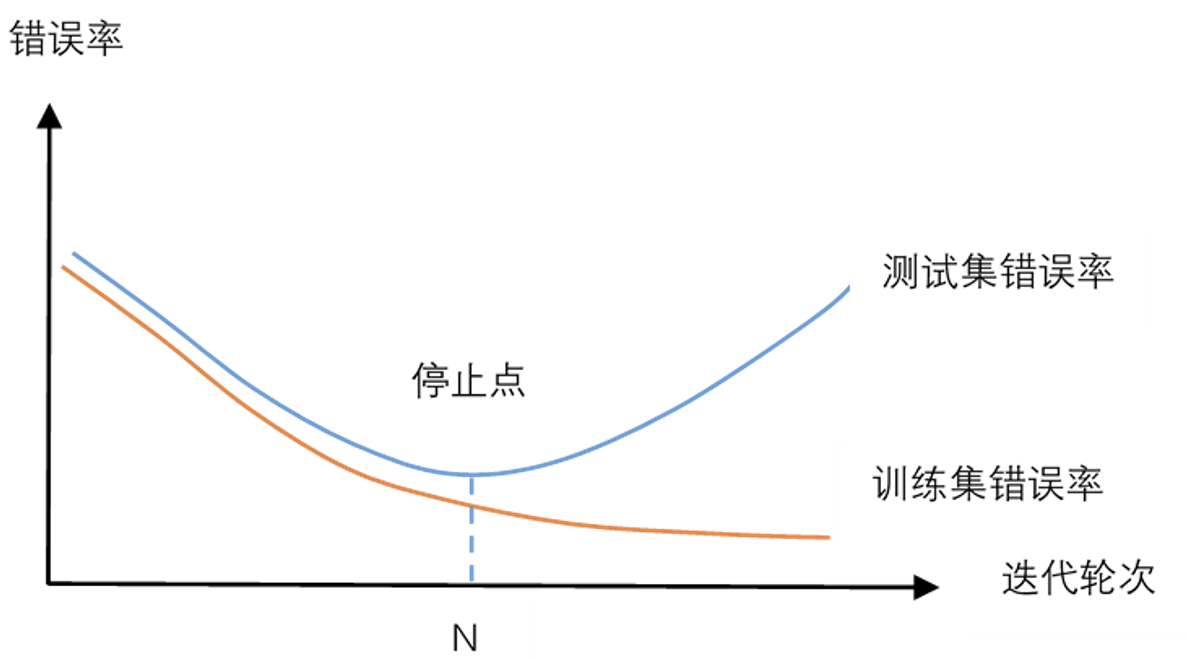
• 使用验证集: 用于调整超参数.

• 限制模型的复杂性:

  • 正则化项法: 考虑误差平方和损失函数:

    $$E_d(w)=\sum_{k=1}^{m}(t_{kd}-o_{kd})^2.$$

    加入正则化项用于降低模型复杂性:

    $$E_d(w)=\sum_{k=1}^{m}(t_{kd}-o_{kd})^2+\Vert w\Vert_2^2.$$

    • 2-范数: 很多参数值很小, 但基本不为 0, 抗干扰能力强.

    • 1-范数: 一些参数为 0, 起到特征选择的作用.

  • 舍弃法: 随机地临时舍弃一些神经元.

• 增加数据量: 获得更多的数据.

  • 数据增强法: 数据越多, 过拟合的风险就越小.

词向量

• 神经网络处理文本 (词&文本) 的方法.

• 独热编码 (one-hot): 用与词表等长的向量表示一个词, 只有一个元素为 1.

  • 优点: 编码简单.
  • 缺点: 编码太长, 无法度量词之间的相似性 (例: 2-范数度量).

• 分布式表示: 相比于独热编码, 是一种稠密表示.

  

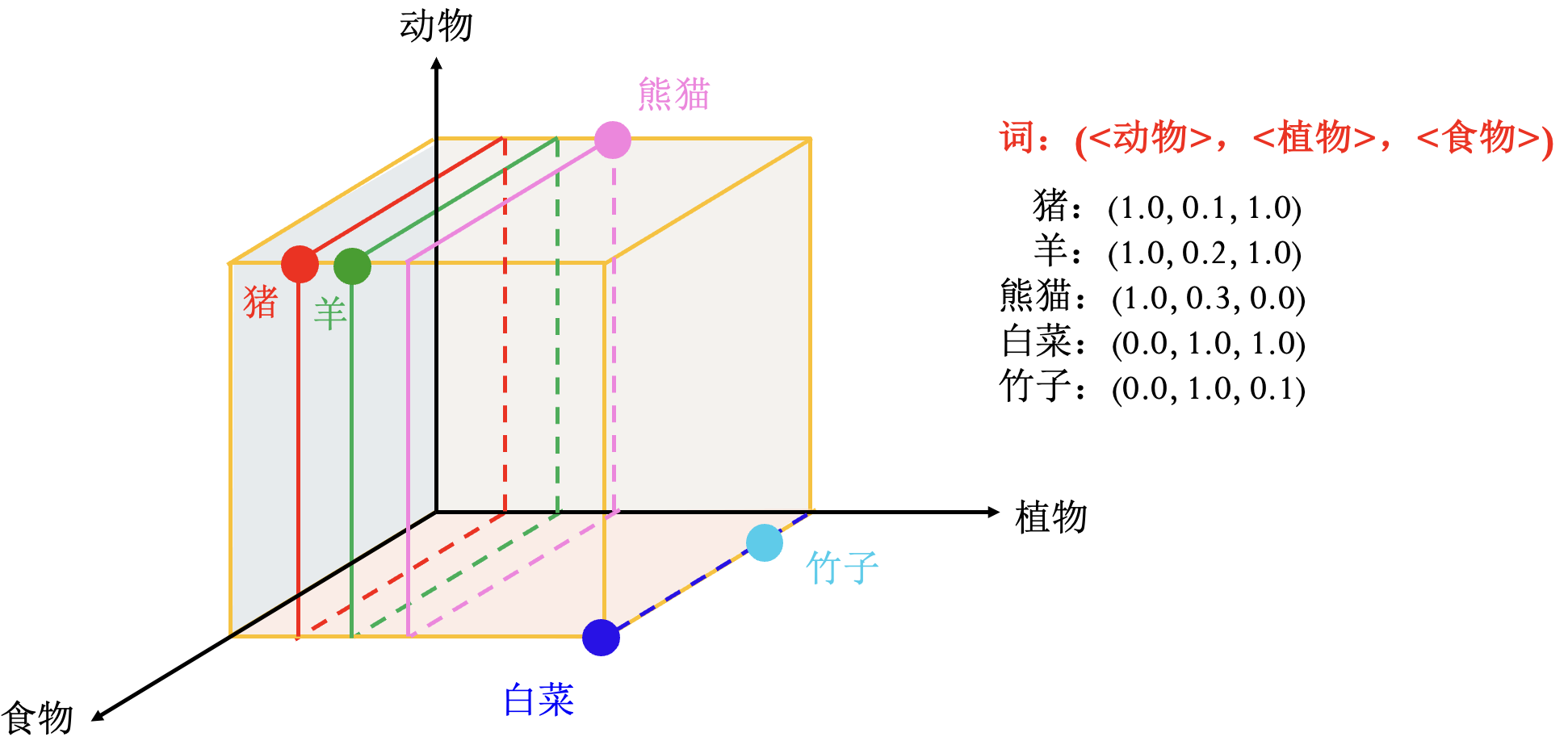
• 词嵌入: 把词向量从高维空间嵌入到低维空间中的一个方法.

• 神经网络语言模型: 用神经网络实现的语言模型.

  

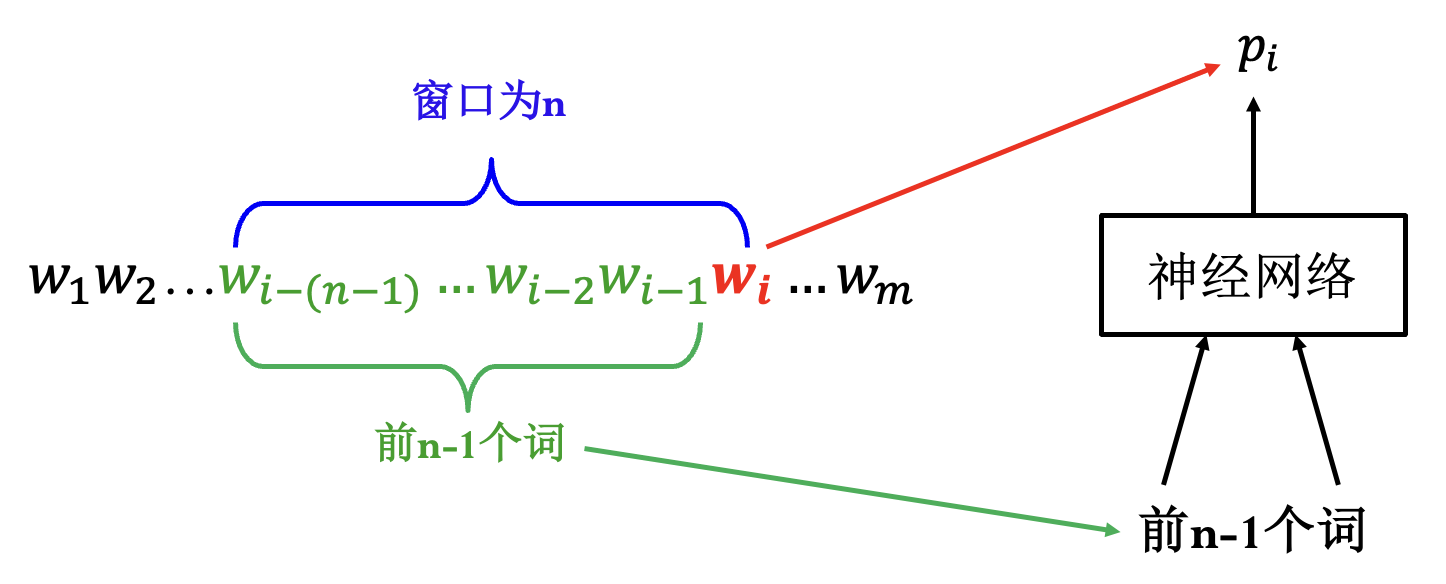
  标准的全连接网络 (前向神经网络):

  

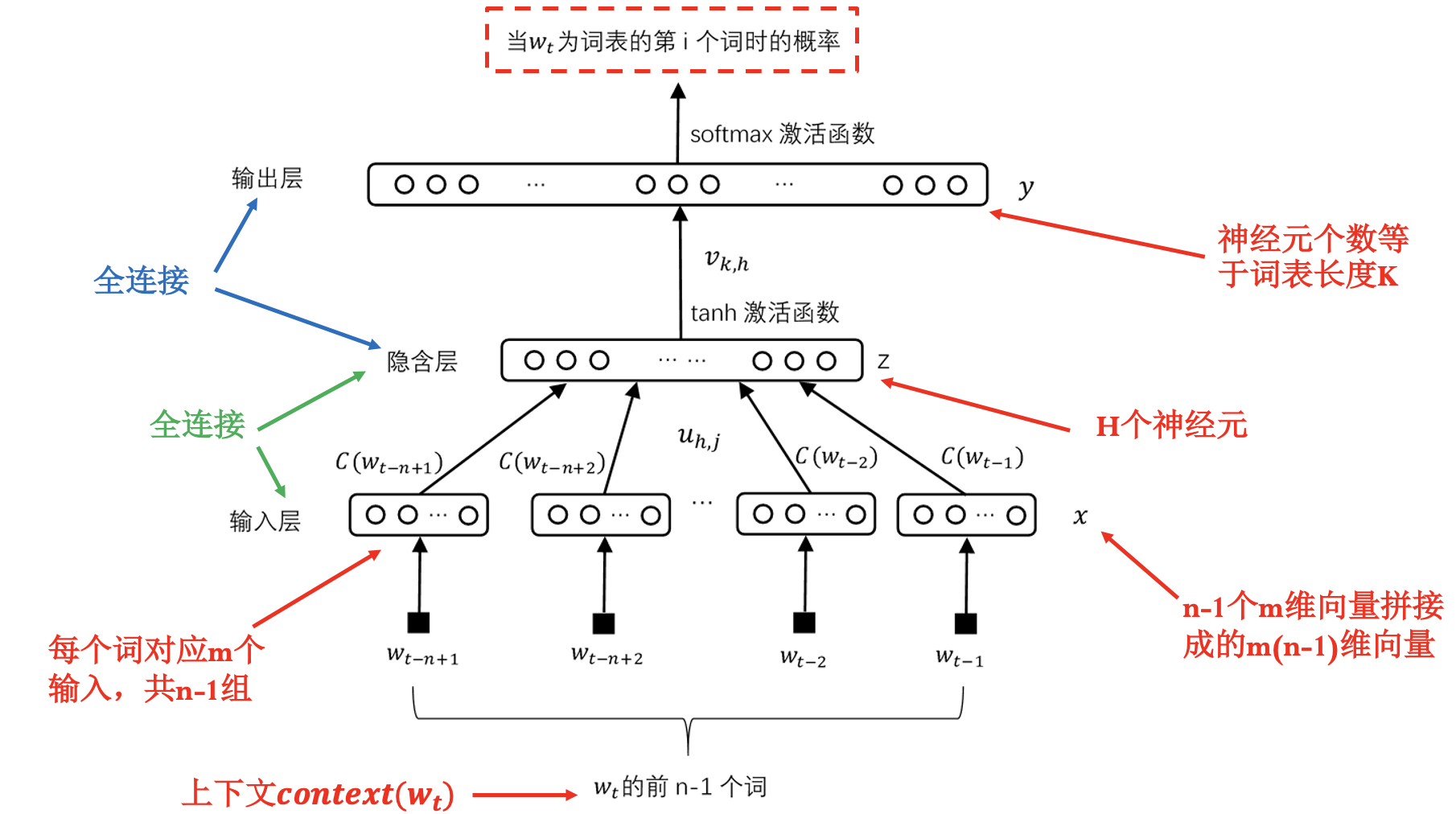
  语言模型同时训练词向量和权重:

  

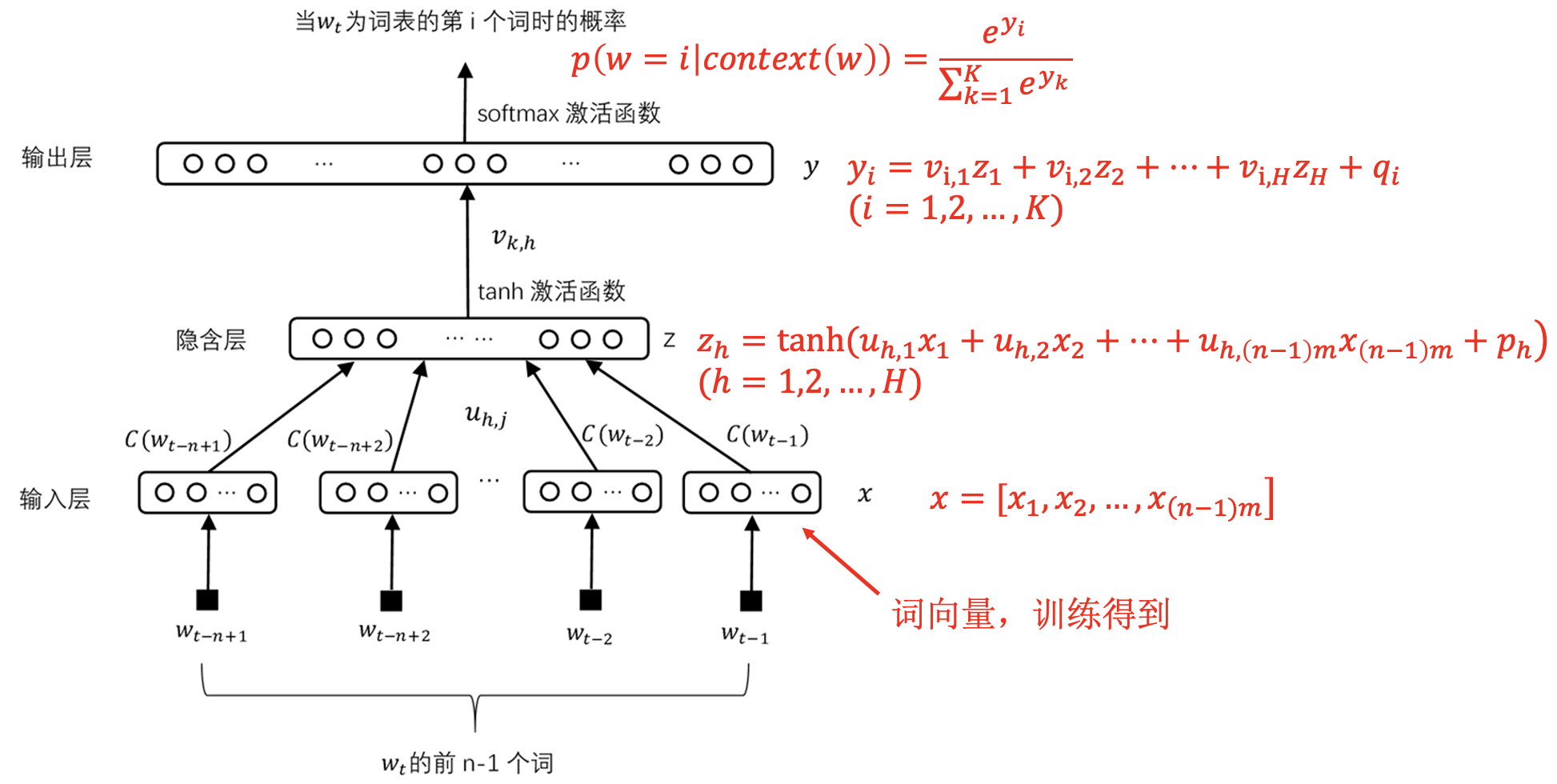
• 训练神经网络语言模型: 让联合概率最大化估计概率 (最大似然估计).

  • 联合概率分布一般含有参数.

  • 通过最大似然方法估计联合概率的参数.

  • 对于神经网络语言模型, 即是估计网络的参数值.

  • 损失函数 (负对数似然函数):

    $$-\sum_{w\in C}\log p(w=k\mid context(w),\theta).$$

    其中 $\theta$ 表示神经网络的所有参数, $C$ 为语料库.

  • 存在问题:

    • 神经元个数等于词表长度 $K$.
    • $m(n-1)$ 个输入, 全连接参数多.

• 训练词向量:

  

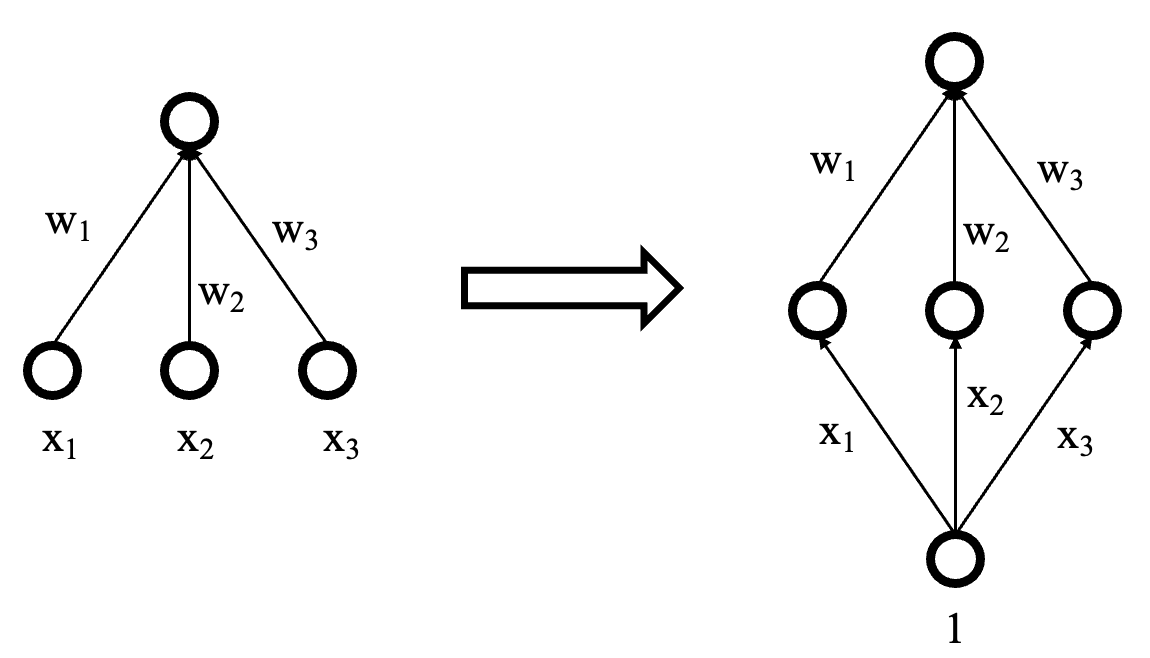
  每个词随机给定词向量, 并在进行训练实时更新 (输入层相当于一个新增的隐含层). 通过训练语言模型, 得到词向量 (自监督).

• word2vec模型: 一种简化的神经网络语言模型.

  • 连续词袋模型 (CBOW): 不考虑上下文中词的顺序.

    

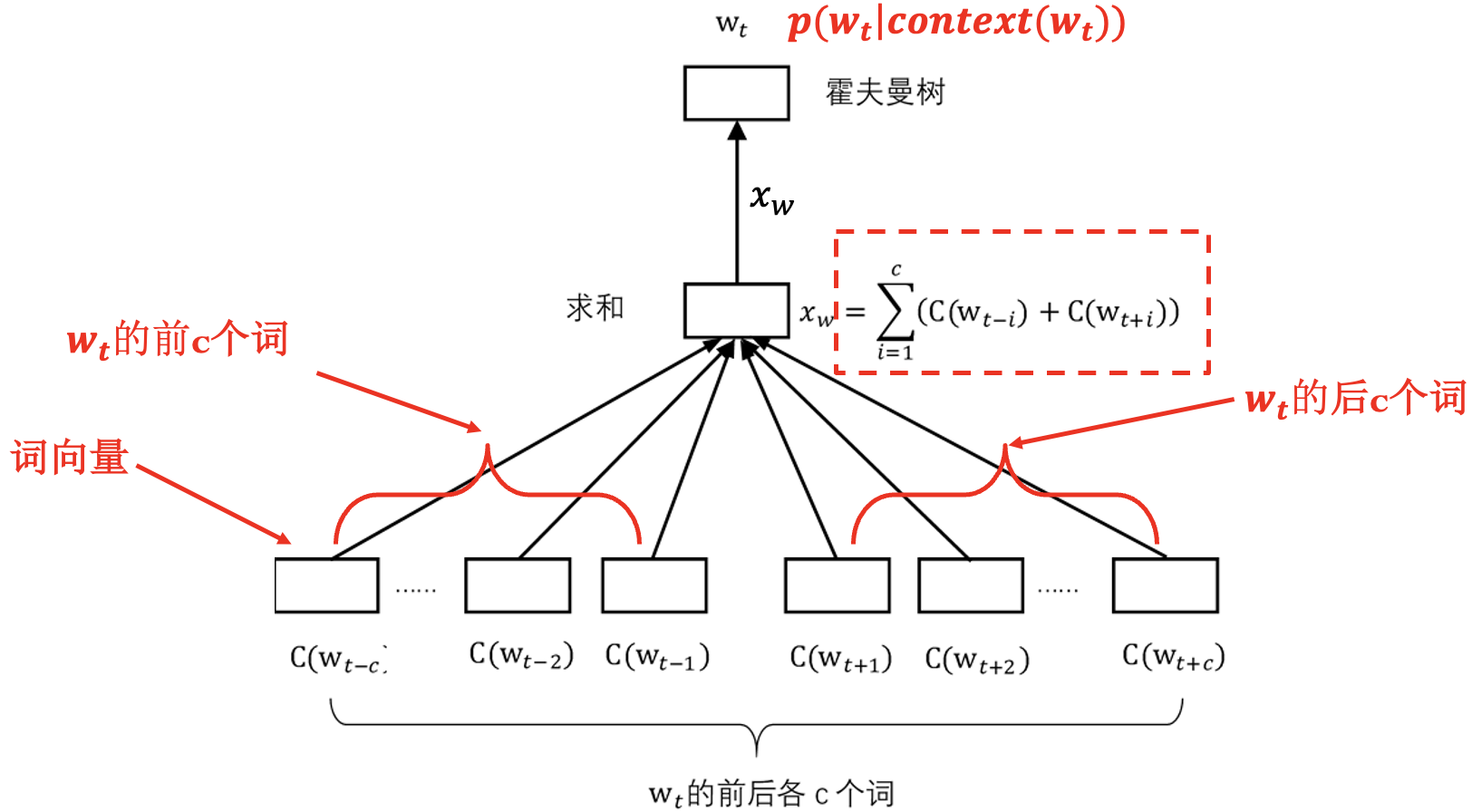
    输出处理得到的 $x_w$ 的长度即为一个词向量的长度, 使用语料库预生成的 Huffman Tree 替换隐含层及输出层. 每次训练时只计算与该词有关的参数, 且越是常用词涉及的参数越少, 训练速度快.

    $W$ 经过霍夫曼树每个节点时的概率为:

    $$p(d_i^w\mid x_w,\theta_{𝑖−1}^w)= \begin{cases} \sigma(x_w\cdot\theta_{𝑖−1}^w), & d_i^w=0\\ 1-\sigma(x_w\cdot\theta_{𝑖−1}^w), & d_i^w=1 \end{cases}$$

    其损失函数:

    $$L=-\sum_{i=2}^{l_w}\{(1-d_i^w)\log{[\sigma(x_w\cdot\theta_{𝑖−1}^w)]}+d_i^w\log{[1-\sigma(x_w\cdot\theta_{𝑖−1}^w)]}\}.$$
  • 跳词模型 (Skip-Gram Model).

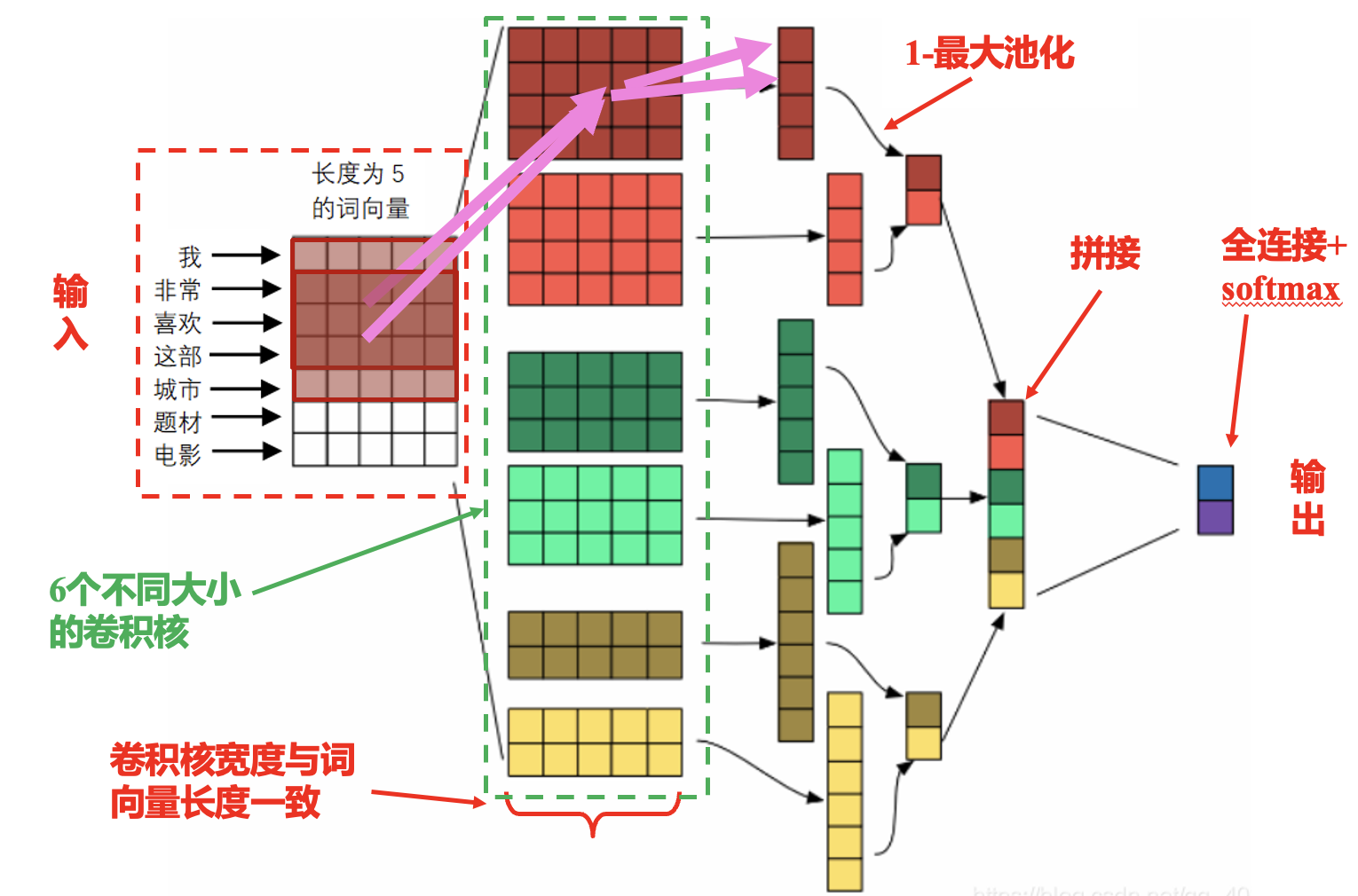
• TextCNN: 词向量应用——情感分类问题.

  

循环神经网络 (RNN)

• 网络辨析:

  • 数据角度:

    • 序列数据.
    • 数据之间有先后联系.

  • 网络结构角度:

    • 前馈网络 (CNN).
    • 反馈网络 (RNN).

  • 表示角度:

    • 句子向量、序列向量.

• 循环模块:

  

  

  

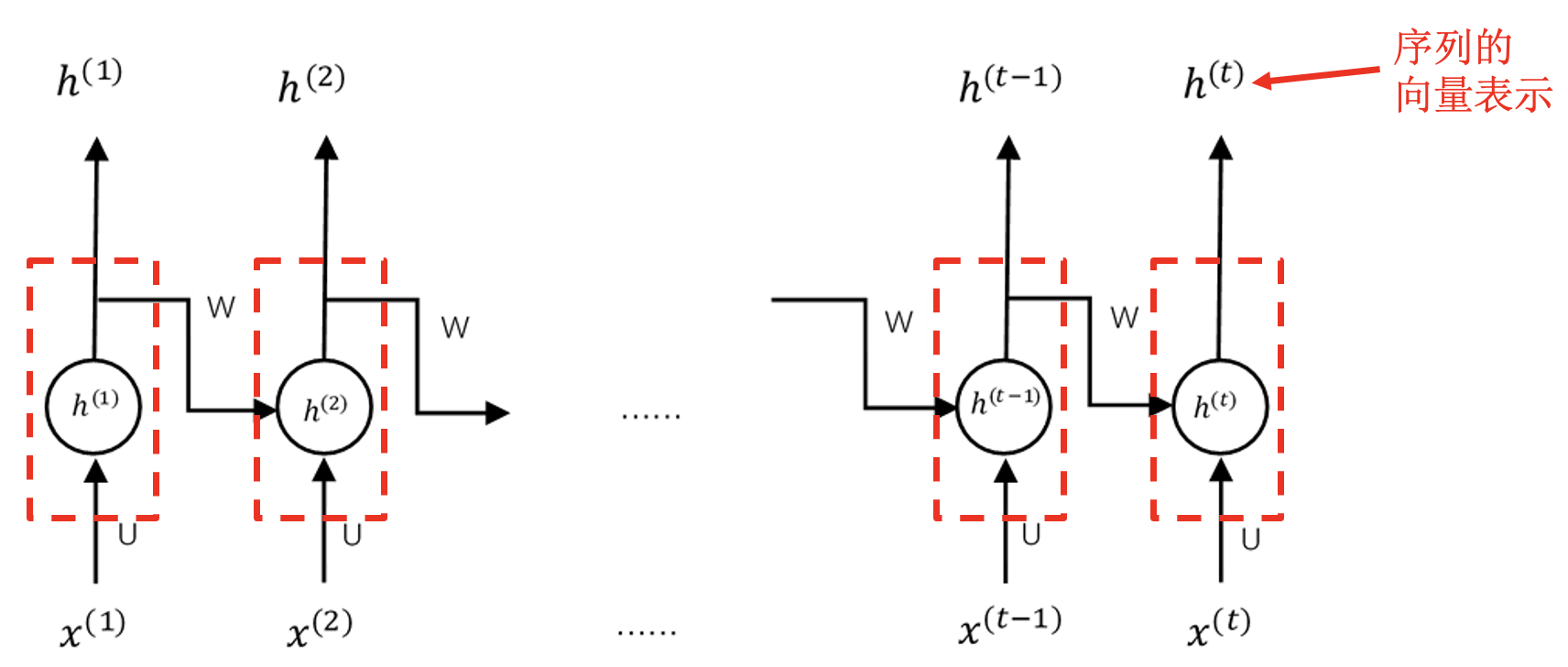
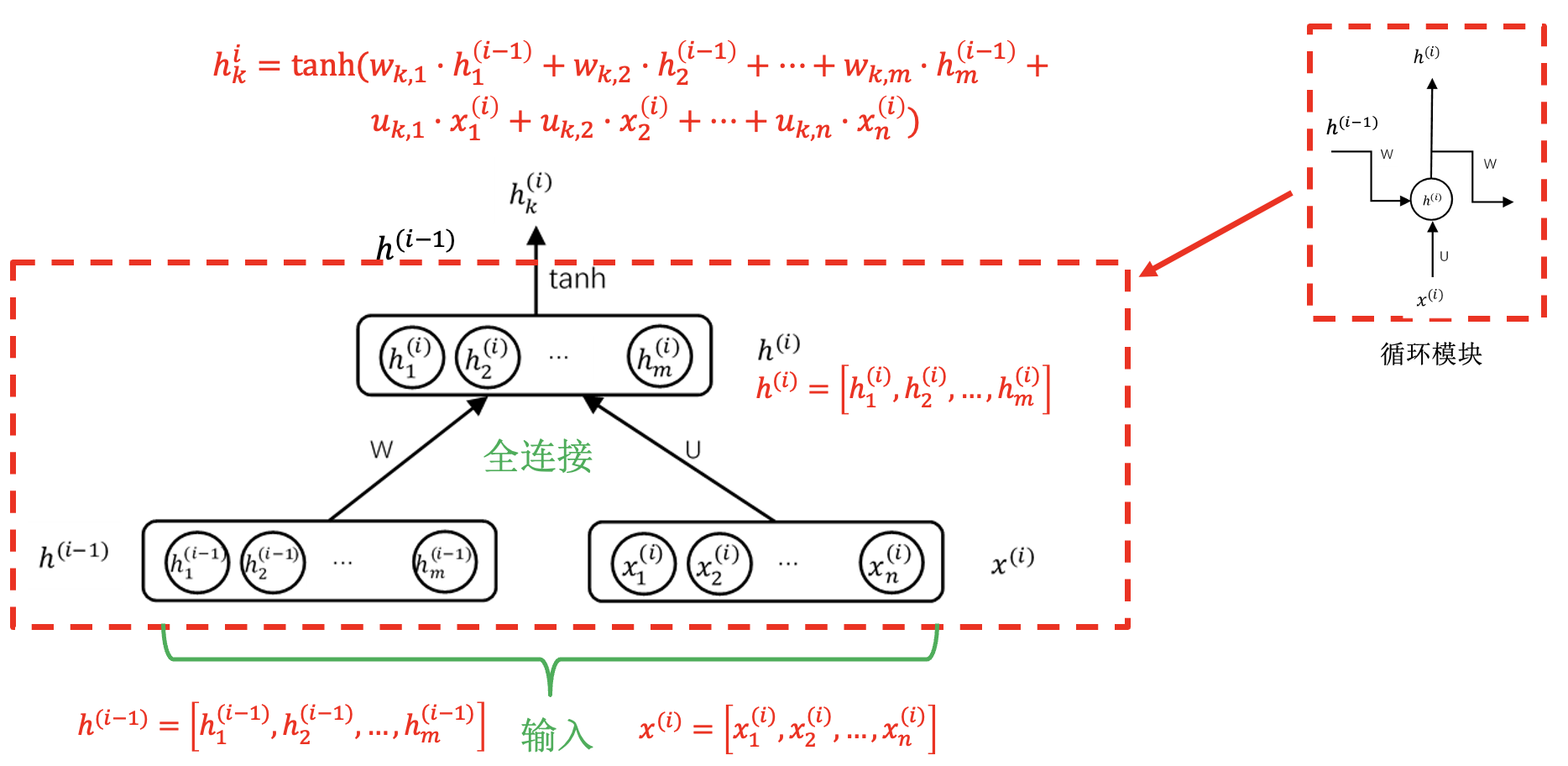
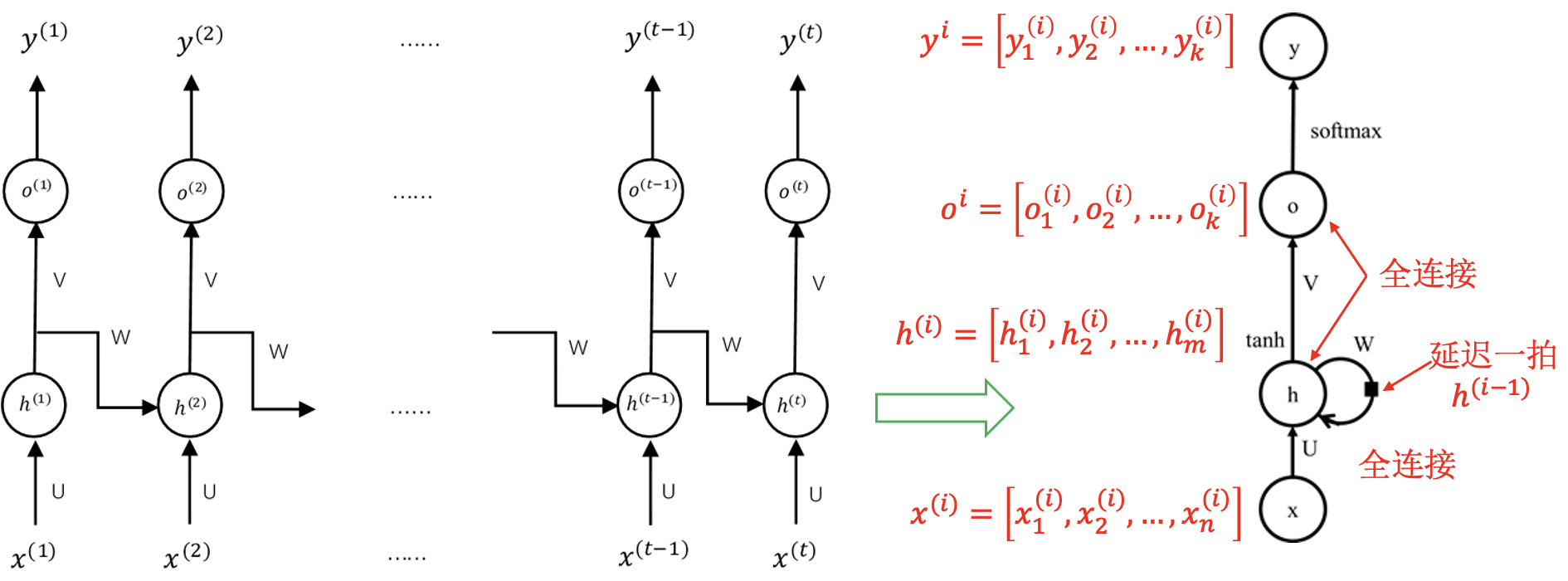
• 循环神经网络的训练: 与具体任务结合.

  

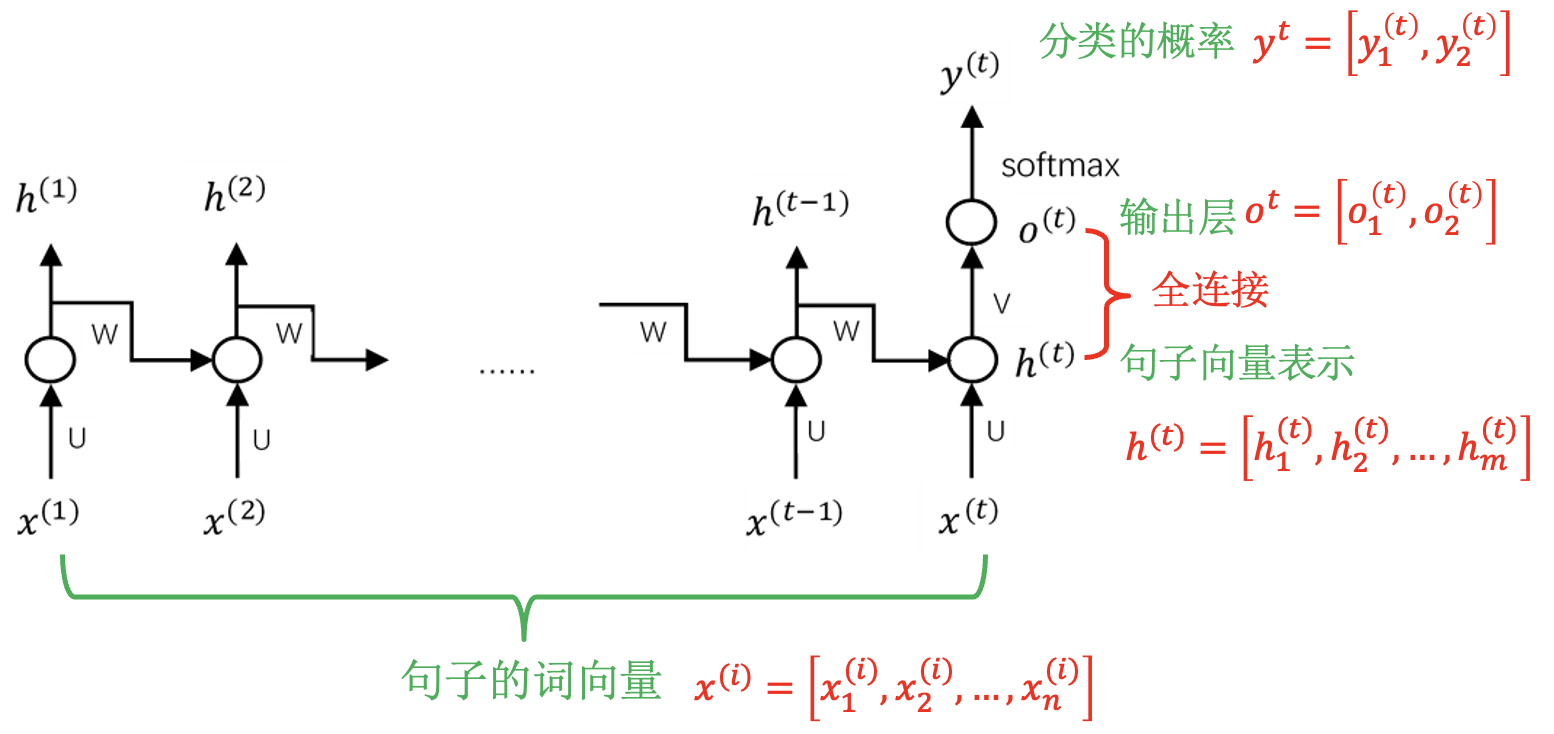
• 例: 看图说话问题

  

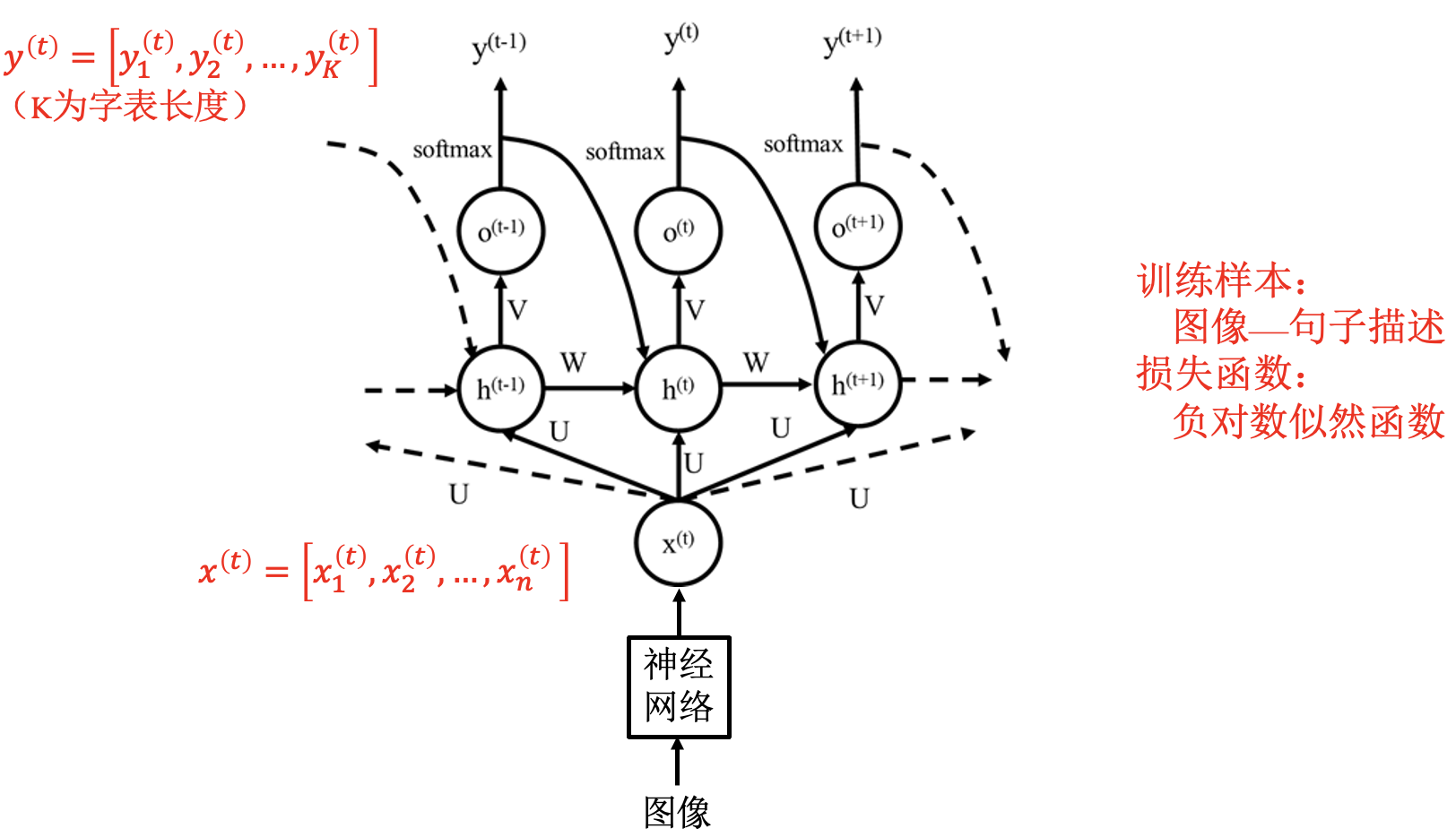
• 双向循环神经网络: 防止序列前面的内容被后面的内容淹没.

  

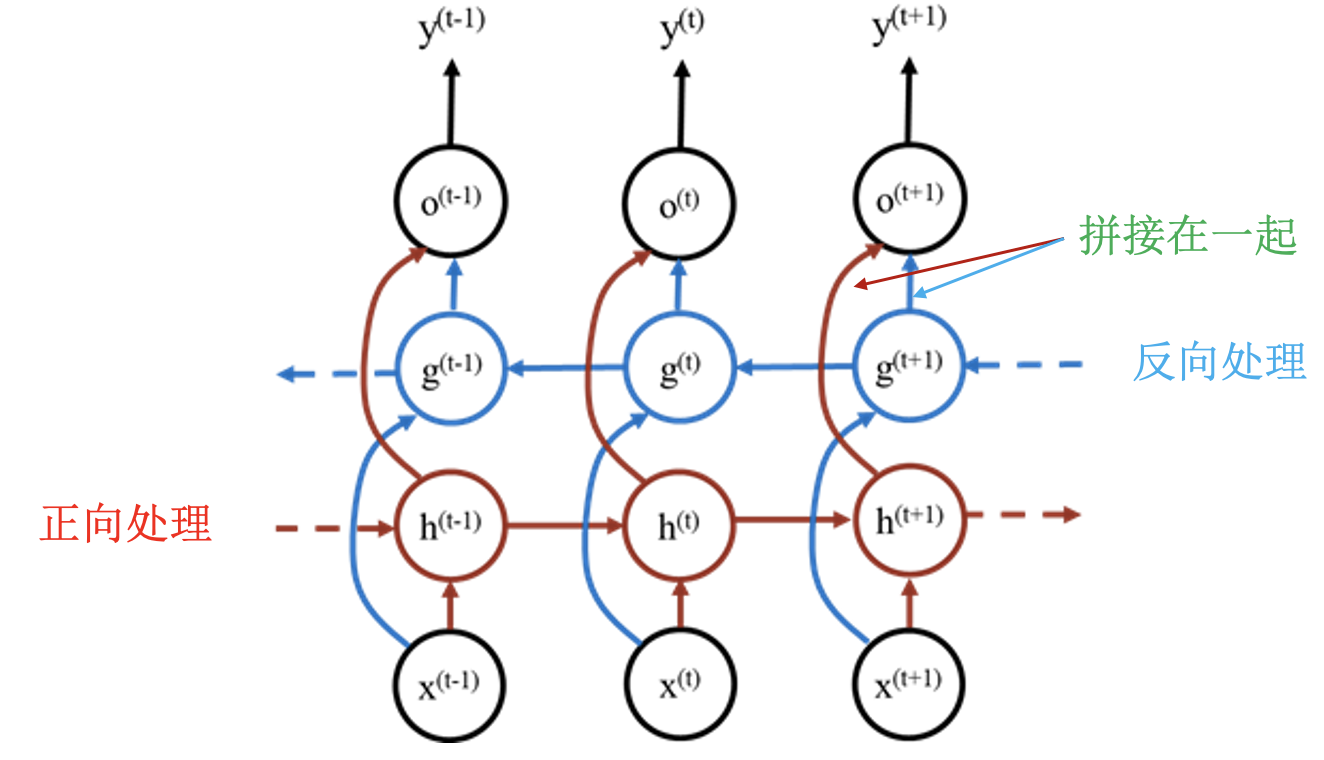
• 序列到序列循环神经网络: 机器翻译、问答系统.

  

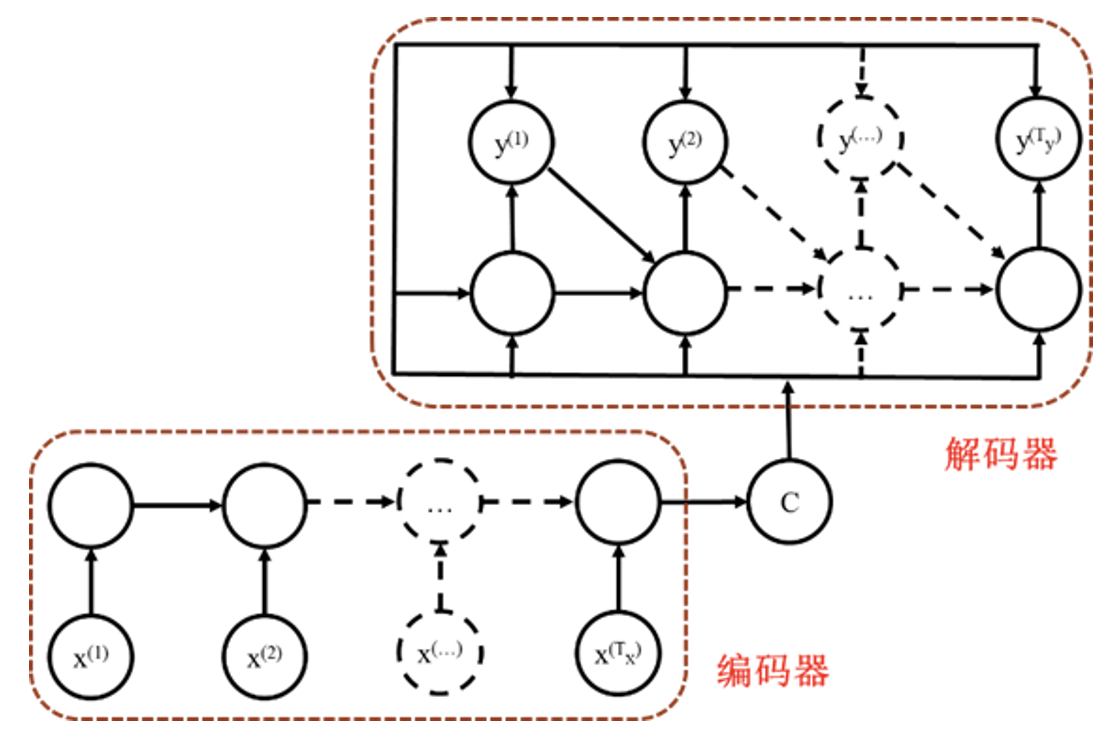
长短期记忆网络 (LSTM)

• 简单 RNN 存在的问题:

  • 长期依赖问题.
  • 重点选择问题: 不同的任务词的重要性不同.

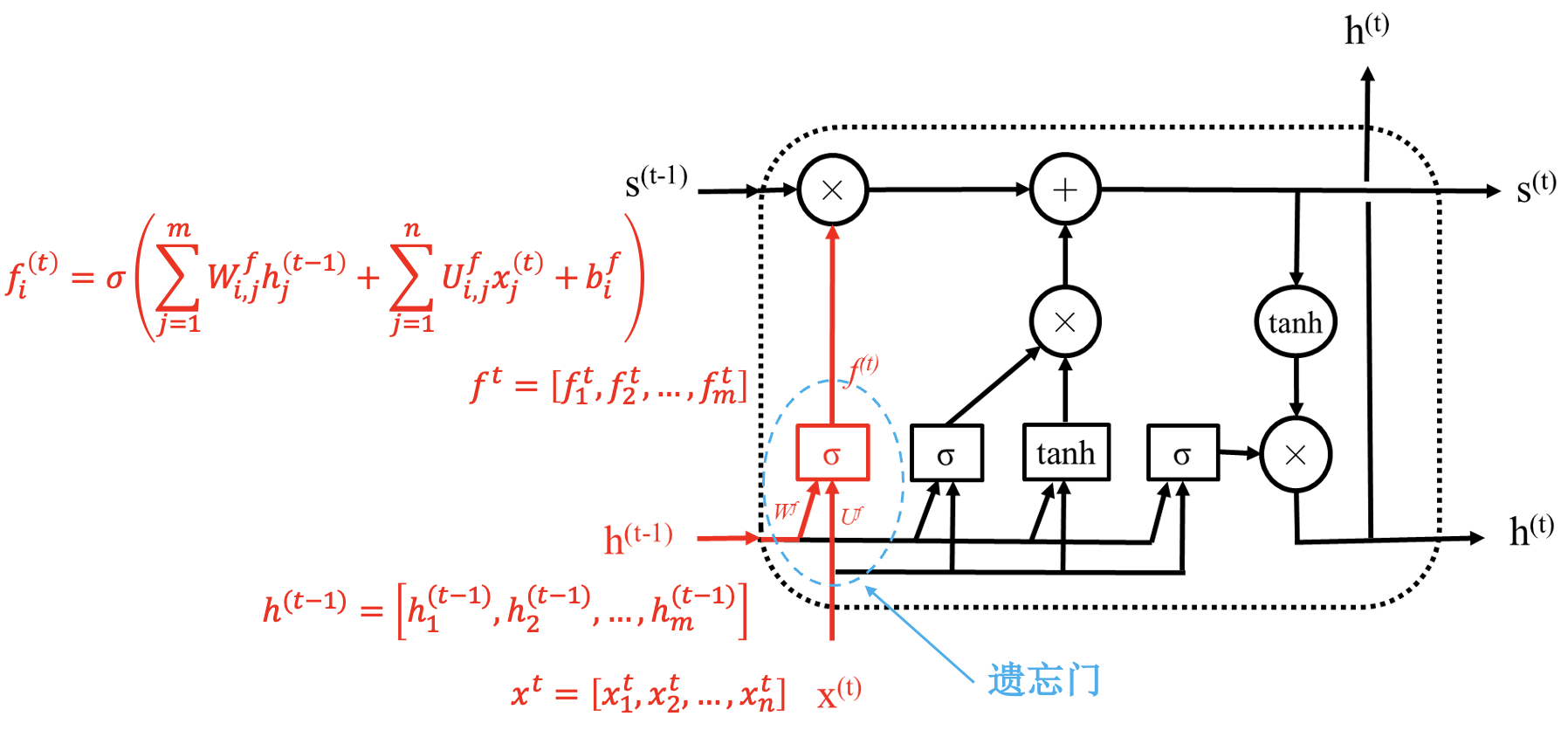
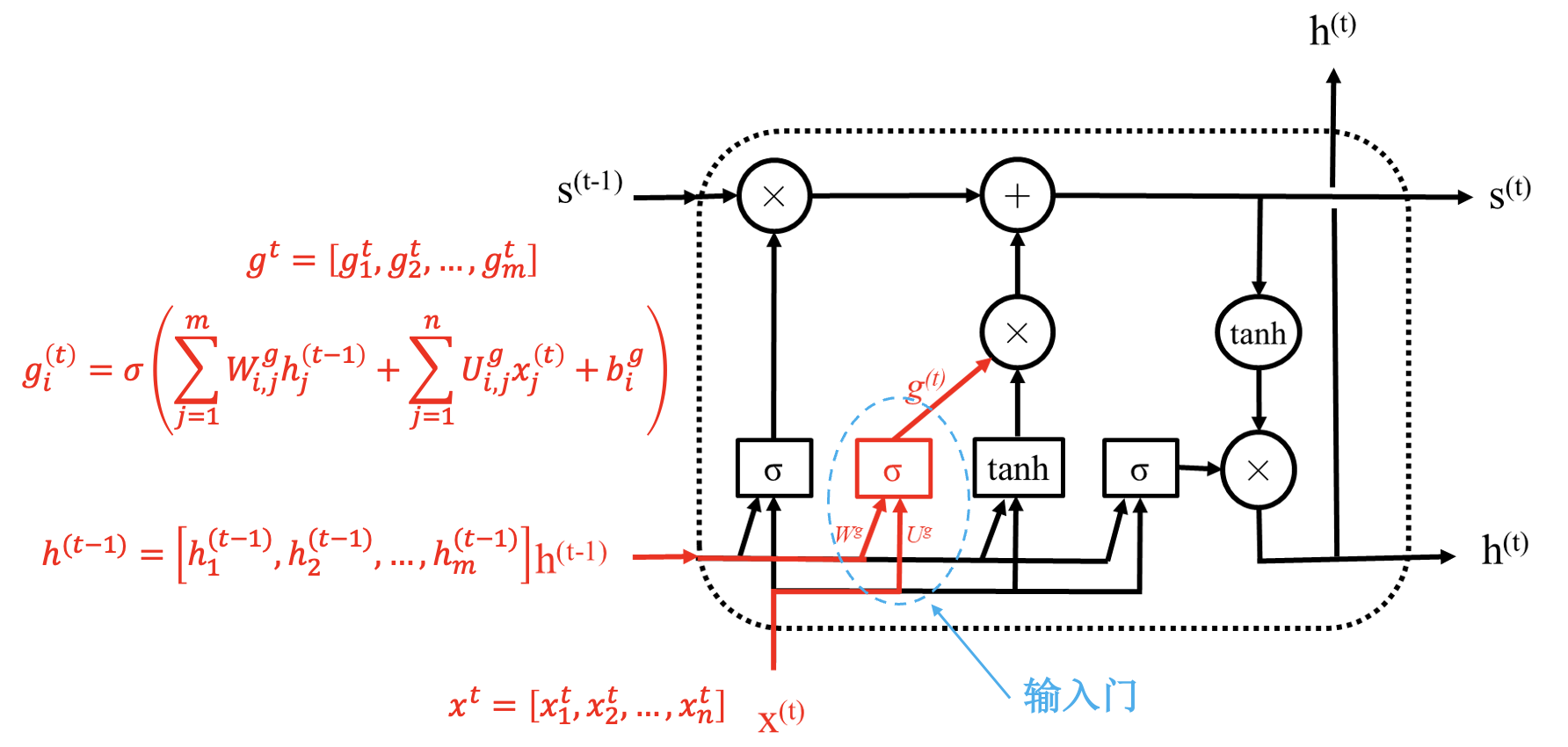
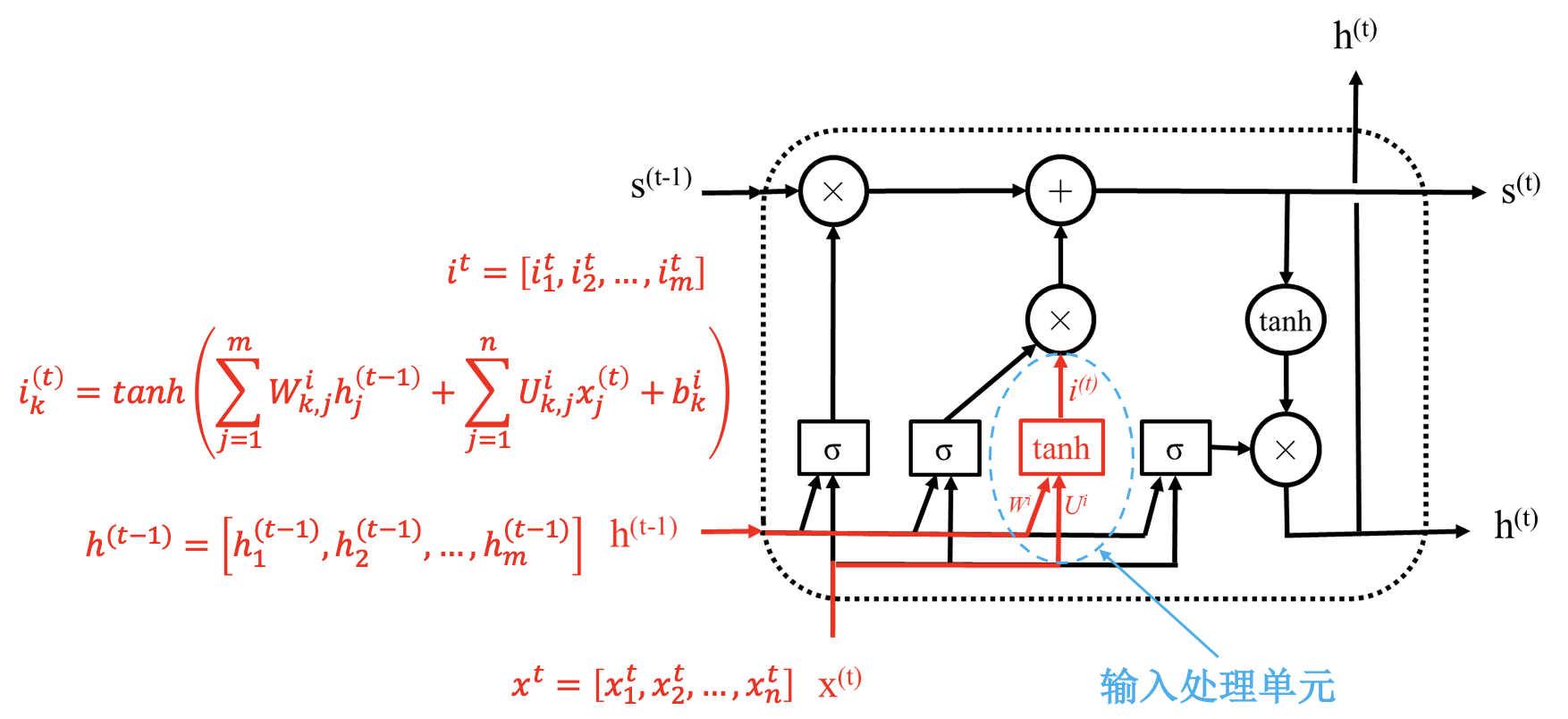
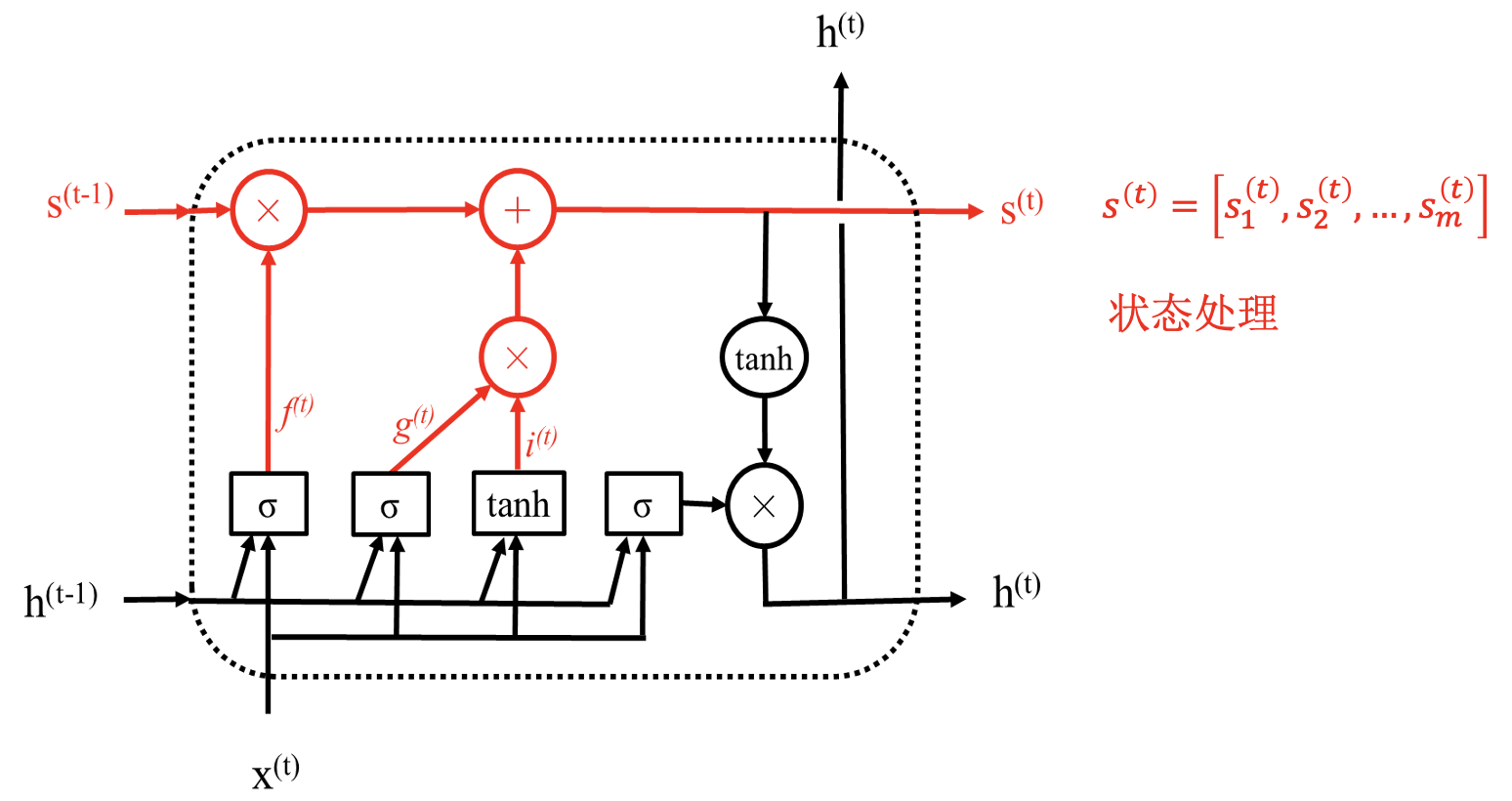
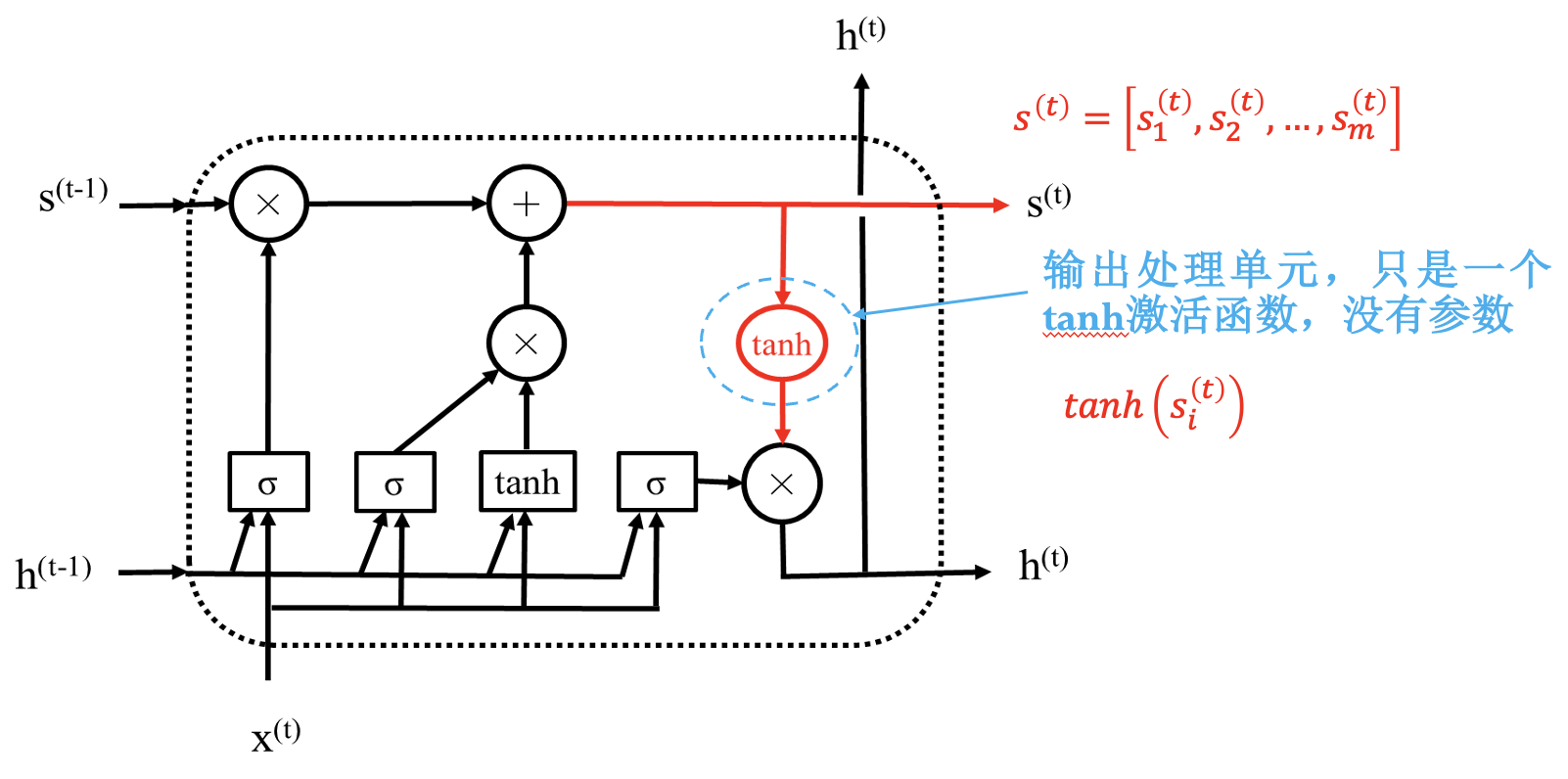
• LSTM 模块:

  

  

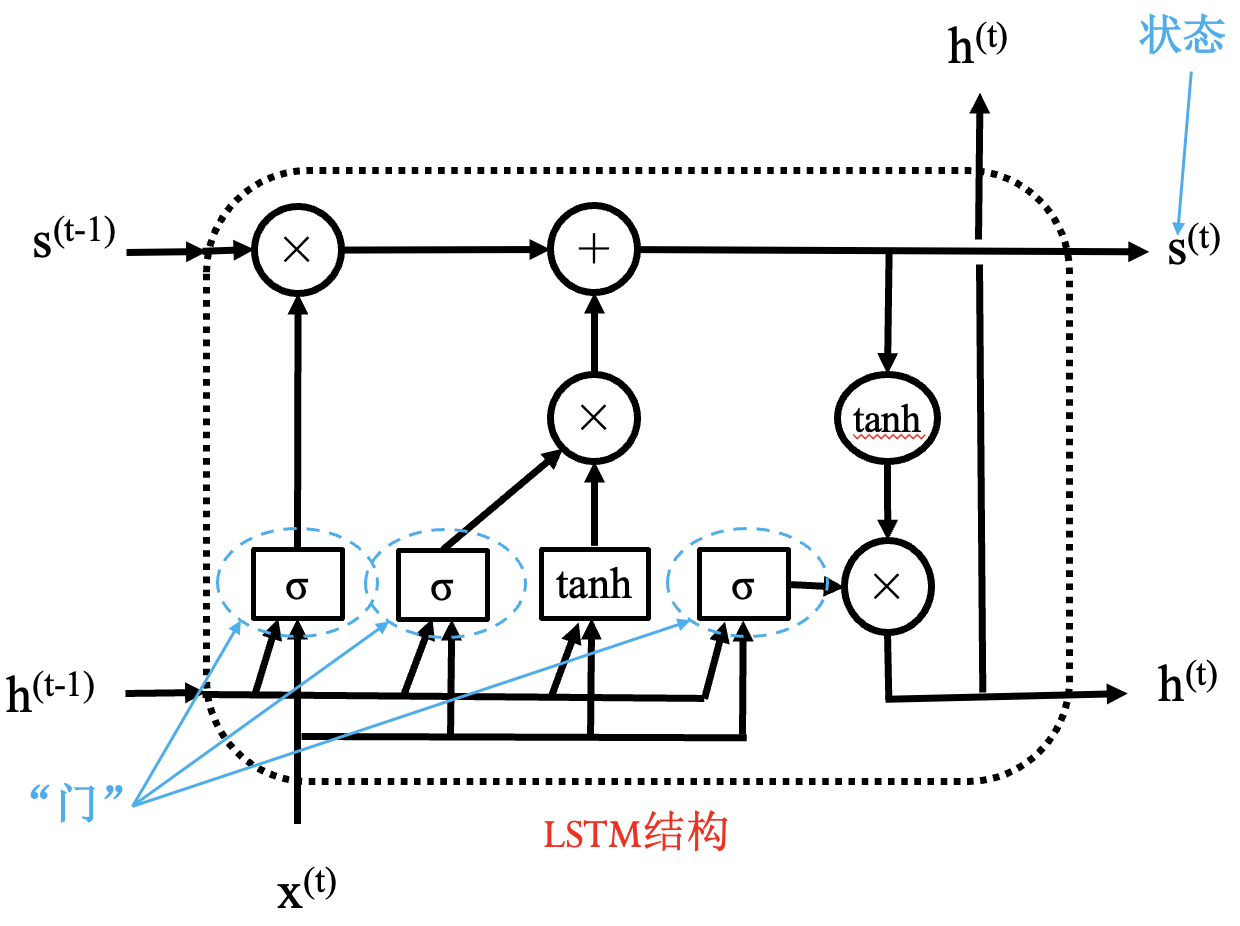
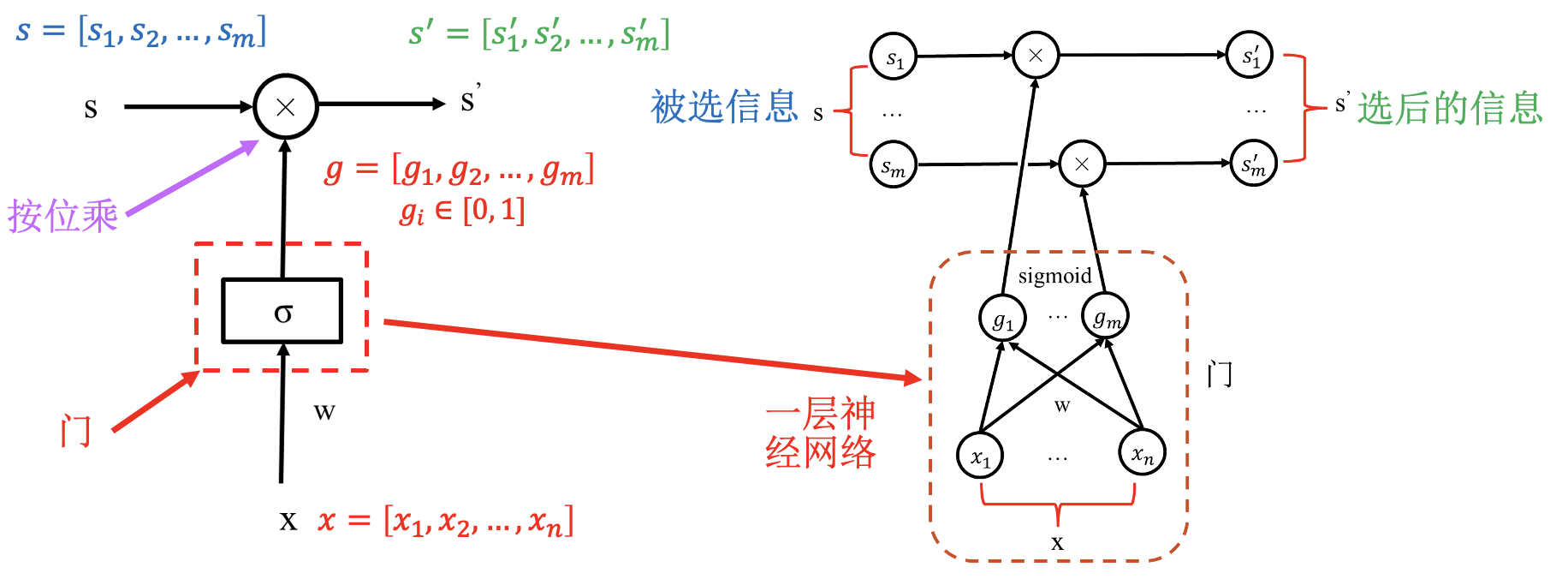
  通过状态解决梯度消失问题; 通过“门”进行选择, 结构一样, 参数不同.

  同简单 RNN 一样, LSTM 模块也是共用的.

• LSTM 具体结构: