第一章搜索问题

深度优先搜索

优先扩展深度深的节点.
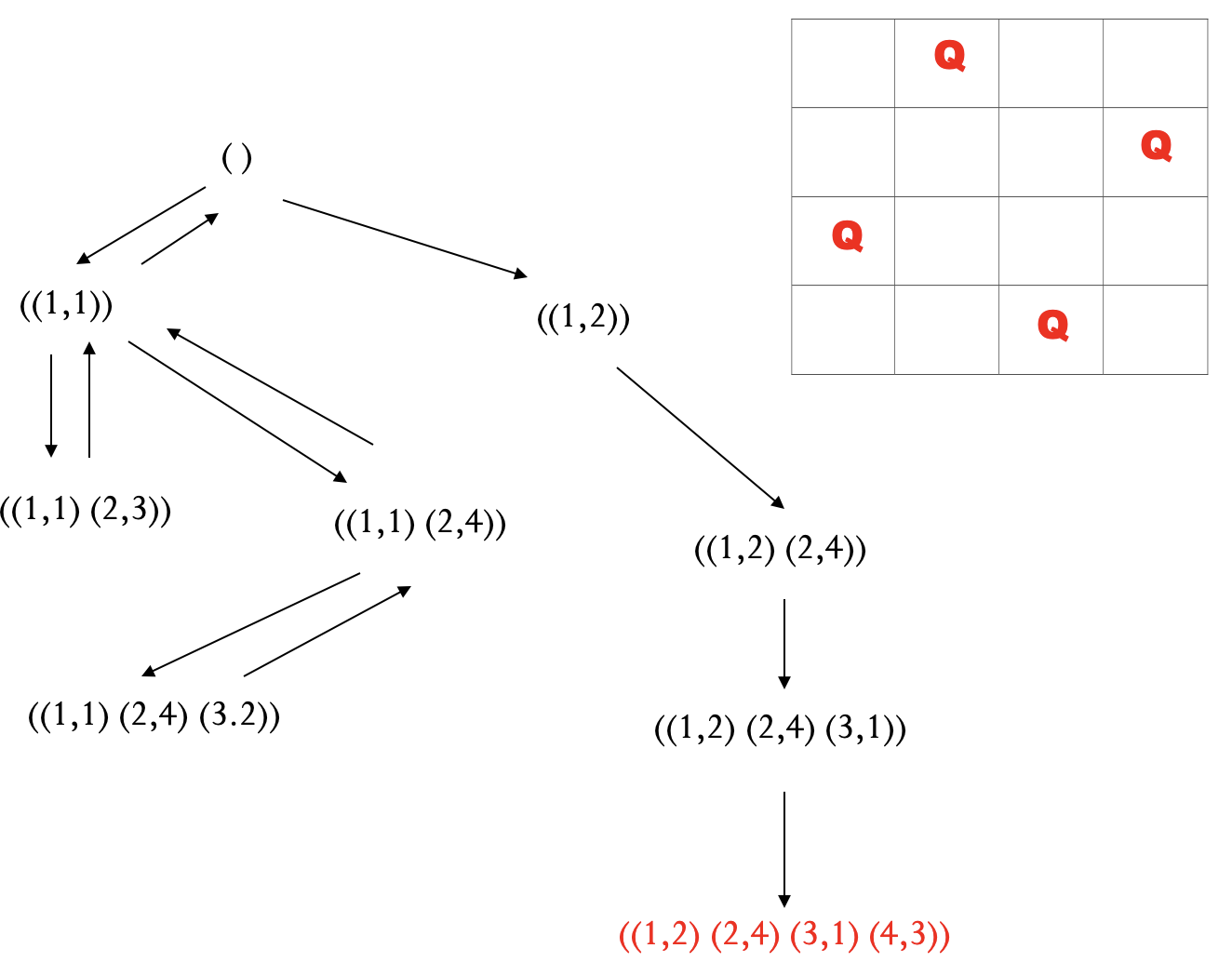
例皇后问题 (深度优先+回溯).
性质:
- 一般不能保证找到最优解.
- 当深度限制不合理时, 可能找不到解, 可以将算法改为可变深度限制.
- 最坏情况时, 搜索空间等同于穷举.
- 是一个通用的与问题无关的方法.
- 节省内存, 只存储从初始节点到当前节点的路径.

宽度优先搜索

优先扩展深度浅的节点.
性质:
- 当问题有解时, 一定能找到解.
- 当问题为单位耗散值, 且问题有解时, 一定能找到最优解.
- 方法与问题无关, 具有通用性.
- 效率较低, 存储量比较大 (带深度模拟的深度优先搜索).

Dijkstra 算法

宽度优先没有考虑两个节点间的距离.
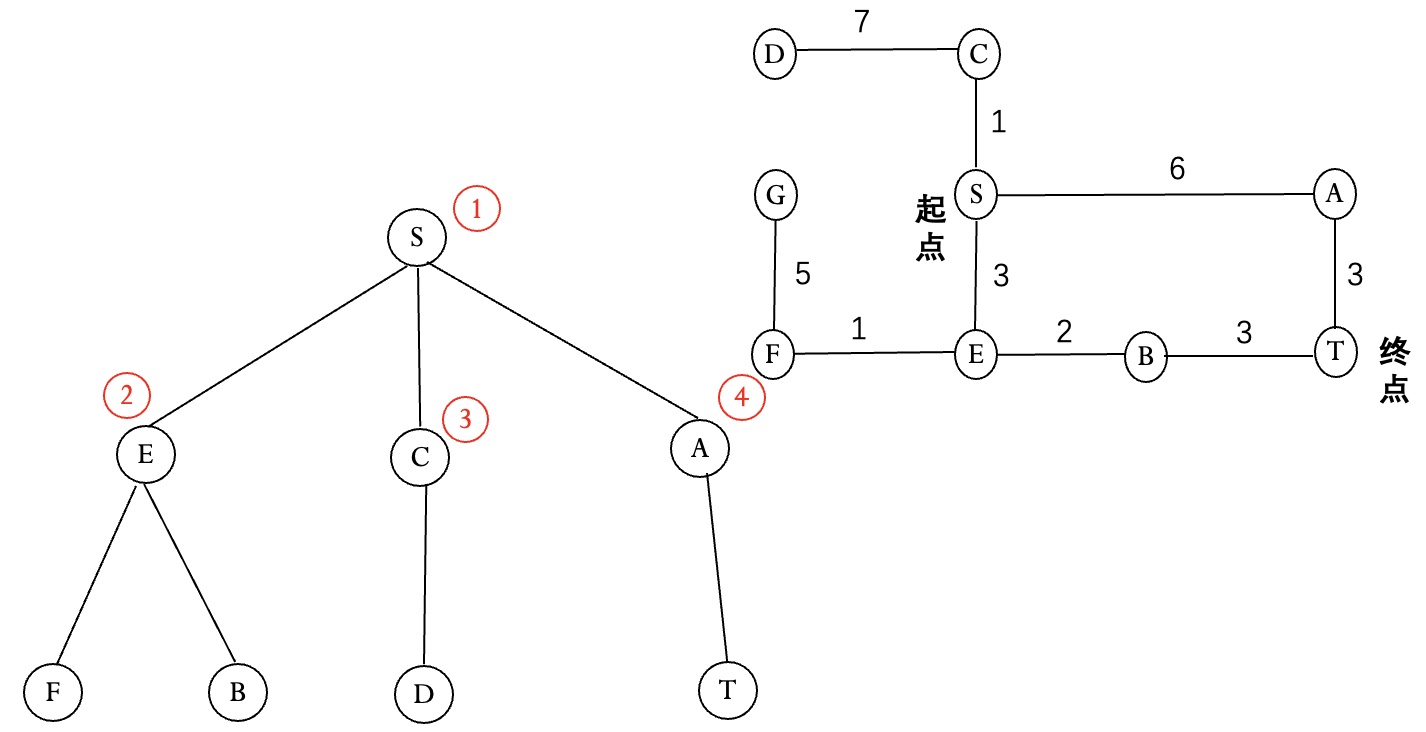
优先扩展距离起点最近的节点, 直到终点距离最短.
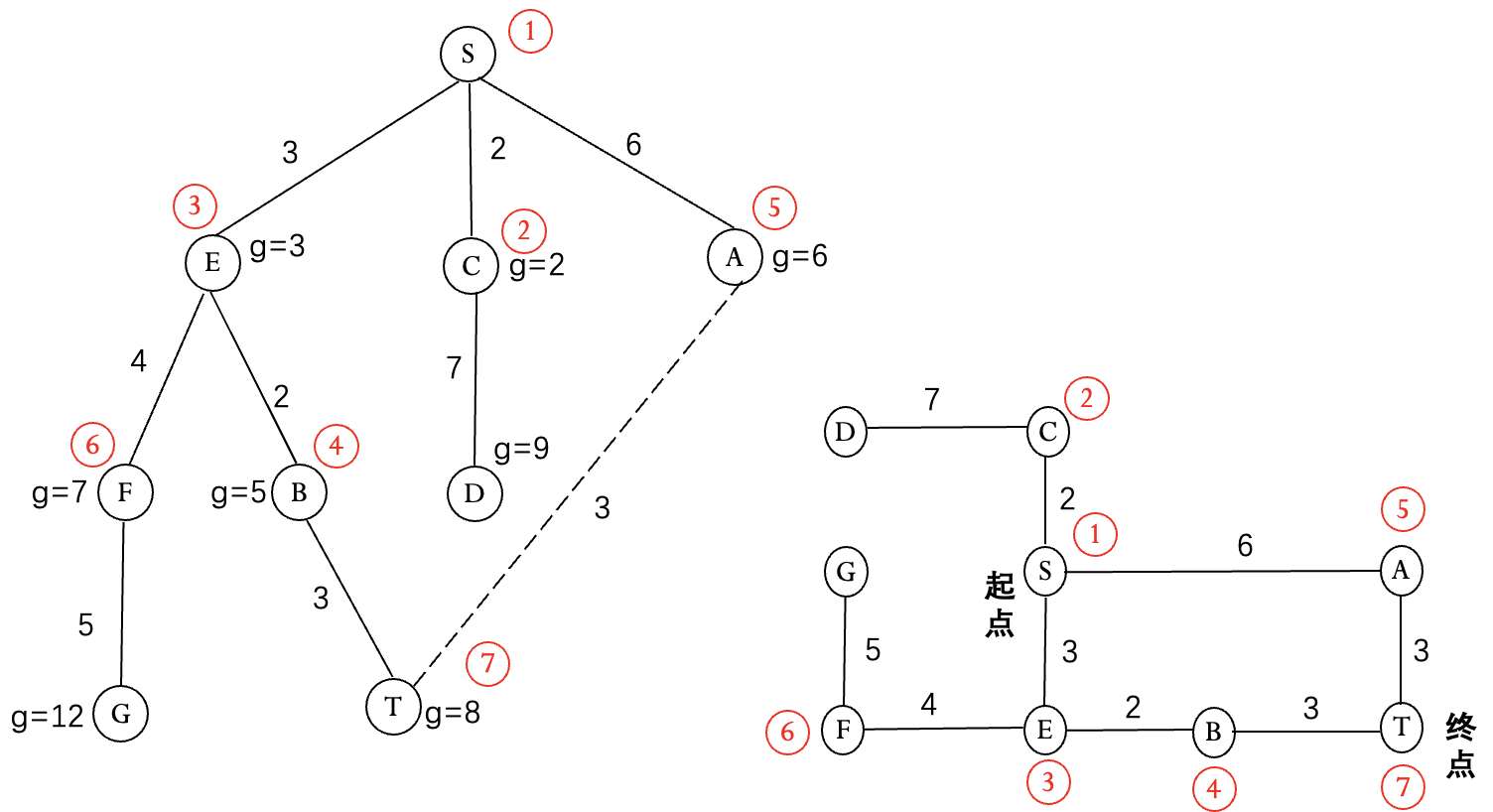
优点: 当问题有解时, 可以找到最佳解.
不足: 只考虑了节点距离起点的距离, 没有考虑节点到终点的距离.

启发式图搜索

引入启发知识, 保证找到最佳解时, 尽可能减少搜索范围, 提高搜索效率.
启发知识: 评估节点到达目标的距离.
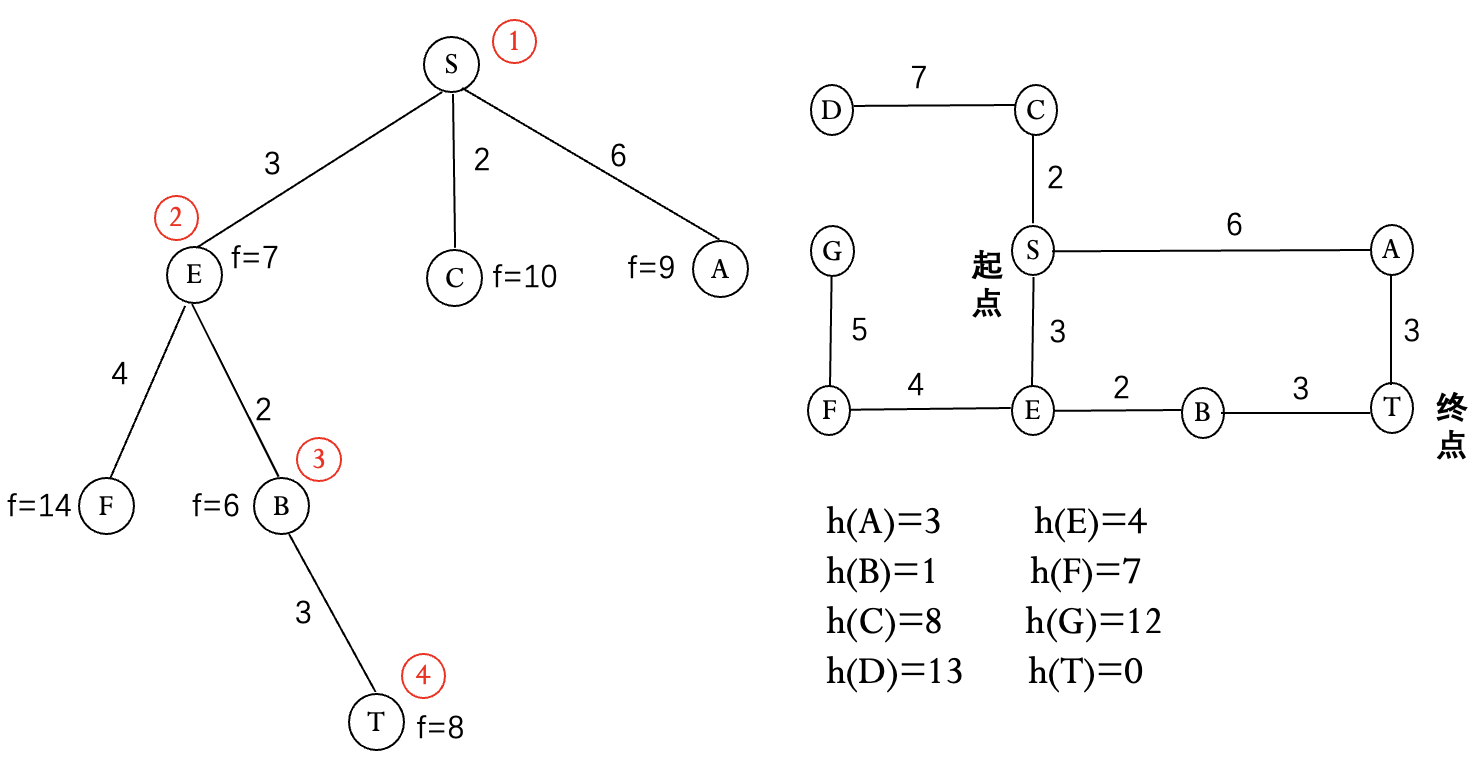
启发式搜索算法 A:
- $g^*(n)$: 从 $s$ 到 $n$ 的最短路径的耗散值.
- $h^*(n)$: 从 $n$ 到 $g$ 的最短路径的耗散值.
- $f^*(n)=g^*(n)+h^*(n)$: 从 $s$ 经过 $n$ 到 $g$ 的最短路径的耗散值.
- $g(n)$, $h(n)$, $f(n)$ 分别是 $g^*(n)$, $h^*(n)$, $f^*(n)$ 的估计值.
- 用 $f(n)$ 对待扩展节点进行评价, 优先扩展 $f(n)$ 值最小的节点, 直到 $f(终点)$ 最小.
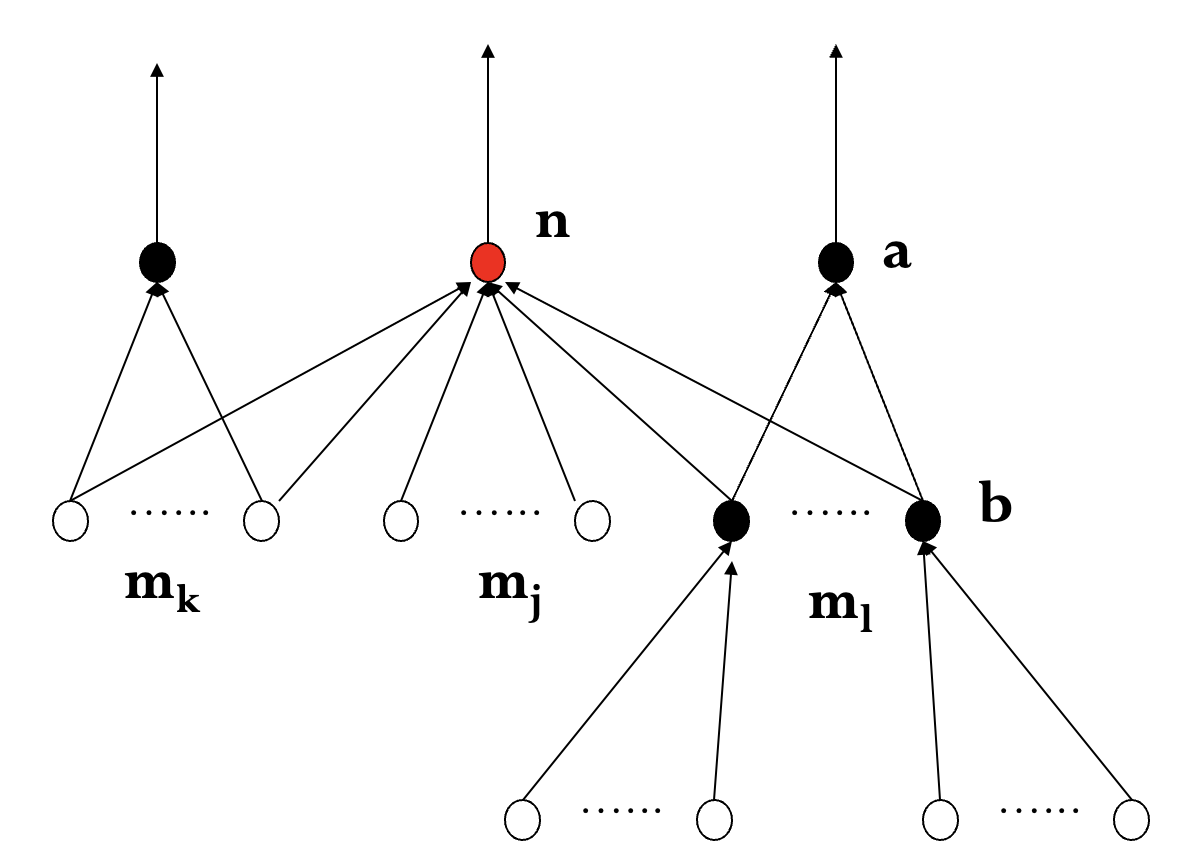
- $m_j$: 扩展时第一次生成, 父节点标记为 $n$.
- $m_k$: 已生成尚未扩展, 比较 $f(m_k)$, $f(n,m_k)$ 决定是否重标记父节点.
- $m_l$: 已生成已扩展, 比较 $f(m_l)$, $f(n,m_l)$ 决定是否重标记父节点, 并重新扩展.
```
# A-algorithm(s): s 为初始节点
OPEN=(s), CLOSED=(), f(s)=g(s)+h(s);
while OPEN 不空 do:
    begin
        n=FIRST(OPEN);
        if GOAL(n) THEN return n;
        REMOVE(n, OPEN), ADD(n, CLOSED);
        EXPAND(n)→{m_i},
	      计算 f(n, m_i)=g(n, m_i)+h(m_i);
			  ADD(m_j, OPEN), 标记 m_j 到 n 的指针;
      	if f(n, m_k)<f(m_k) then 
            f(m_k)=f(n, m_k), 标记 m_k 到 n 的指针;
      	if f(n, m_l)<f(m_l) then 
            f(m_l)=f(n, m_l), 标记 m_l 到 n 的指针,
	       		ADD(m_l, OPEN);
    		OPEN 中的节点按 f 值从小到大排序;
   	end while
return FAIL;
```
- 从目标开始, 顺序访问父节点, 直到初始节点, 得到解路径.
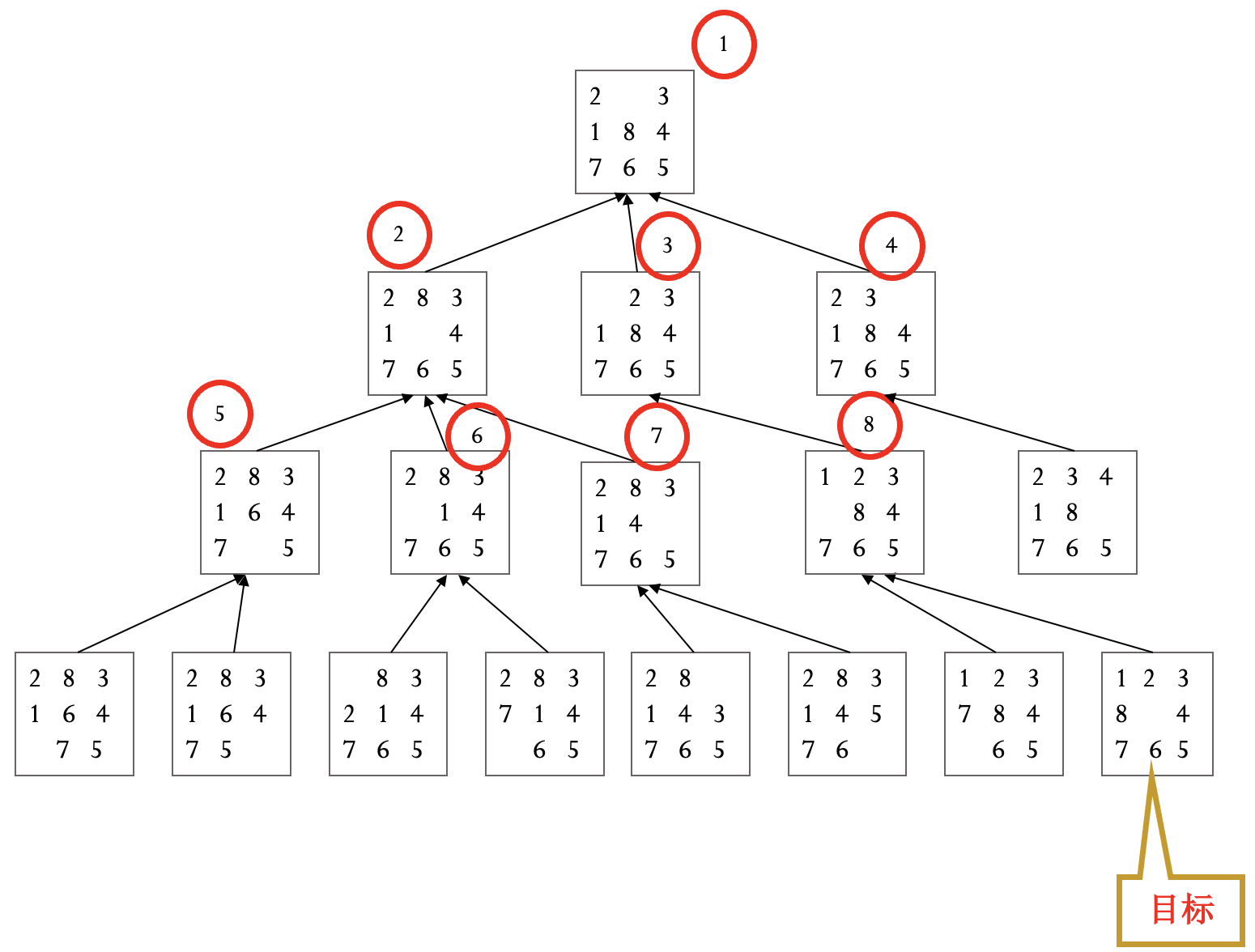
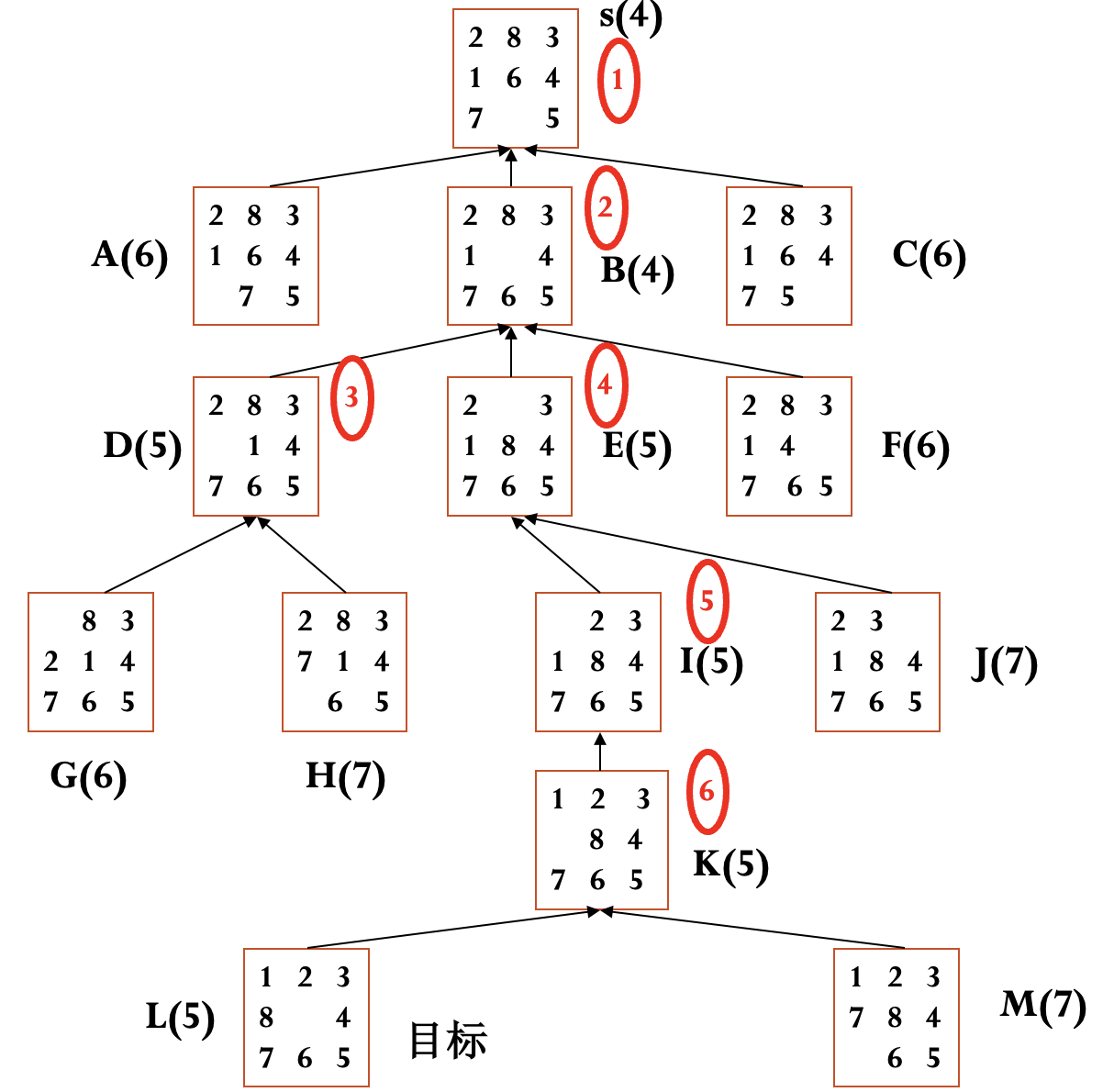
- 例(八数码问题) 定义 $g(n)$ 为到当前节点的耗散值, $h(n)$ 为当前节点不在位的将牌数.
最佳图搜索算法 A*:
- 在 A 算法中, 如果满足条件:
  $h(n)\le h^*(n)$
  则 A 算法称为 A* 算法.
- 例(八数码问题) 定义 $h_1(n)$ 为当前节点不在位的将牌数, $h_2(n)$ 为当前节点将牌不在位的距离和, 注意到这两种定义均满足 A* 算法的条件.
- 选取 $h$ 的一般原则: 放宽限制条件, 在宽条件下给出估计函数.
- 定理 1 若存在从初始节点 $s$ 到目标节点 $t$ 有路径, 则 A* 必能找到最佳解结束.
- 定理 2 对同一问题定义两个 A* 算法 A$_1$ 和 A$_2$, 若 A$_2$ 比 A$_1$ 有较多的启发信息, 即对所有非目标节点有 $h_2(n)>h_1(n)$, 则在具有一条从 $s$ 到 $t$ 的路径的隐含图上, 搜索结束时由 A$_2$ 所扩展的每一个节点, 也必定由 A$_1$ 所扩展, 即 A$_1$ 扩展的节点数 $\ge$ A$_2$ 扩展的节点数 (估计更准确).
  - 上述评价指标是 “扩展的节点数”, 同一个节点只计算一次.
  - 为什么条件不能是 $h_2(n)\ge h_1(n)$? 什么情况下会出现问题? 能否给定理再增加条件, 使得定理在 $h_2(n)\ge h_1(n)$ 条件下也成立?
  - 提示: 考虑那些 $f(n)=f^*(t)$ 的节点, $t$ 为目标节点. 如果不考虑这样的节点, 等号可以加上.
- 对 $h$ 的评价方法: 设共扩展了 $d$ 层节点, 共搜索了 $N$ 个节点, 计算得平均分叉数 $b^*$.
  $N=\dfrac{1-b^{*(d+1)}}{1-b^*}.$
  $b^*$ 越小, 说明 $h$ 效果越好. $b^*$ 是较稳定的常数, 基本不随问题规模变化.
A* 算法的改进:
- 因 A 算法对 $m_l$ 类节点可能要重新放回到 OPEN 表中, 因此可能会导致多次重复扩展同一个节点, 导致搜索效率下降.
- 扩展未找到初始节点到当前节点的最短路径; 距离越近, 估计应越准.
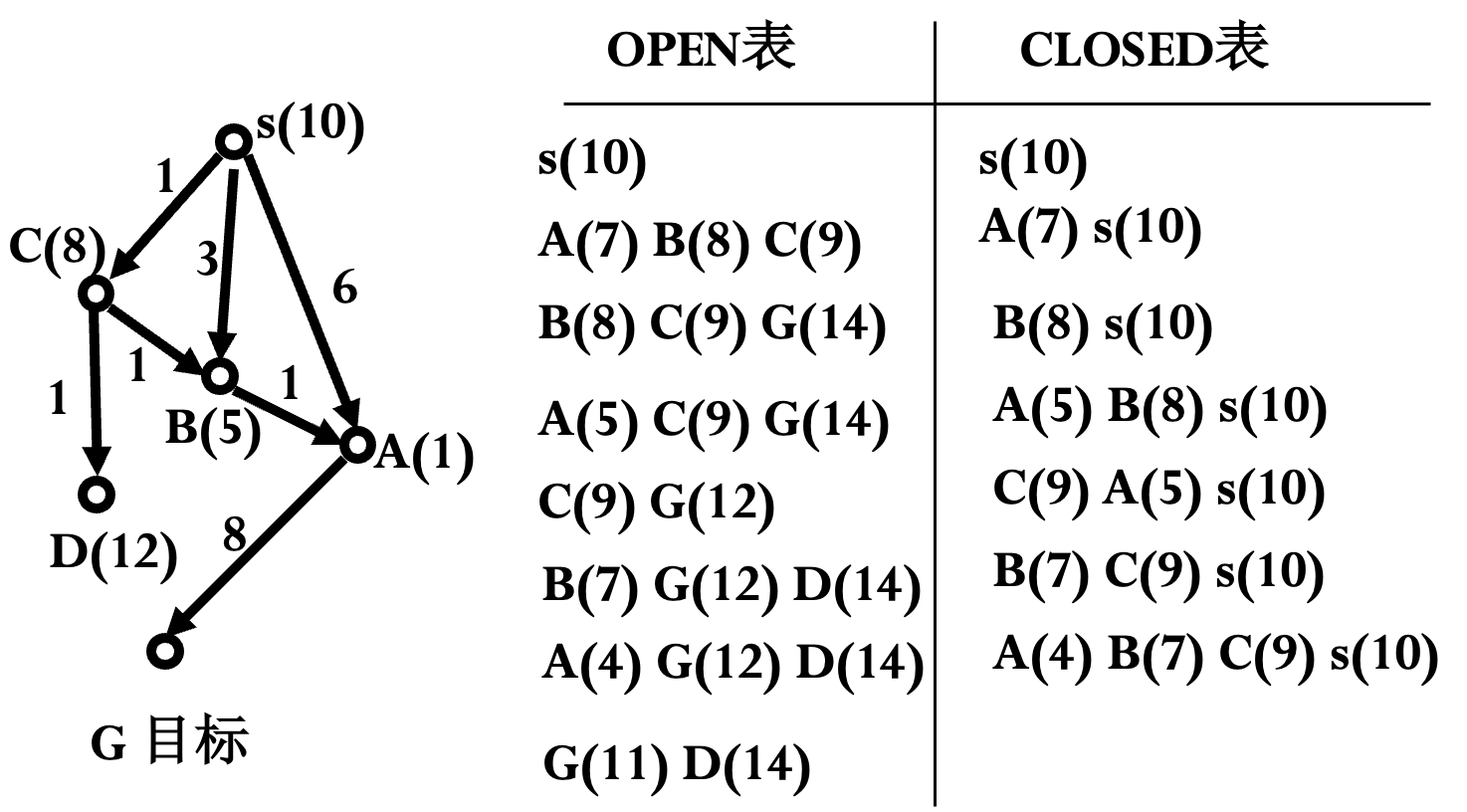
- 对 $h$ 加以限制: 第一次扩展节点时, 就找到了从 $s$ 到该节点的最短路径.
  
  此时称 $h$ 是单调的.
  - 定理若 $h(n)$ 是单调的, 则 A* 扩展了节点 $n$ 之后, 就已经找到了到达节点 $n$ 的最佳路径. 即当 A* 选 $n$ 扩展时, 有 $g(n)=g^*(n)$.
  - 定理当 $h(n)$ 满足单调条件时, 一定满足 A* 条件.
- 对算法加以改进: 避免或减少节点的多次扩展.
  - 定理 OPEN 表上任以具有 $f(n)<f^*(s)$ 的节点定会被 A* 扩展.
  - 定理 A* 选作扩展的任一节点, 定有 $f(n)\le f^*(s)$.
  - 定理当 $h(n)$ 恒等于 0 时, $h$ 为单调的.
```
# Modified-A-algorithm(s): s 为初始节点
OPEN=(s), CLOSED=(), f(s)=g(s)+h(s), f_m=0;
while OPEN 不空 do：
    begin
        NEST={n_i|f(n_i)<f_m,ni->OPEN}
	      if NEST≠( ) then n=NEST 中 g 最小的节点
			        			else n=FIRST(OPEN), f_m=f(n);
        if GOAL(n) THEN return n;
        REMOVE(n, OPEN), ADD(n, CLOSED);
        EXPAND(n →{mi}, 
	     	计算 f(n, m_i)=g(n, m_i)+h(m_i);
			  ADD(m_j, OPEN), 标记 m_j 到 n 的指针;
      	if f(n, m_k)<f(m_k) then 
            f(m_k)=f(n, m_k), 标记 m_k 到 n 的指针;
      	if f(n, m_l)<f(m_l) then 
            f(m_l)=f(n, m_l), 标记 m_l 到 n 的指针,
	       		ADD(m_l, OPEN);
    		OPEN 中的节点按 f 值从小到大排序;
   	end while
return FAIL;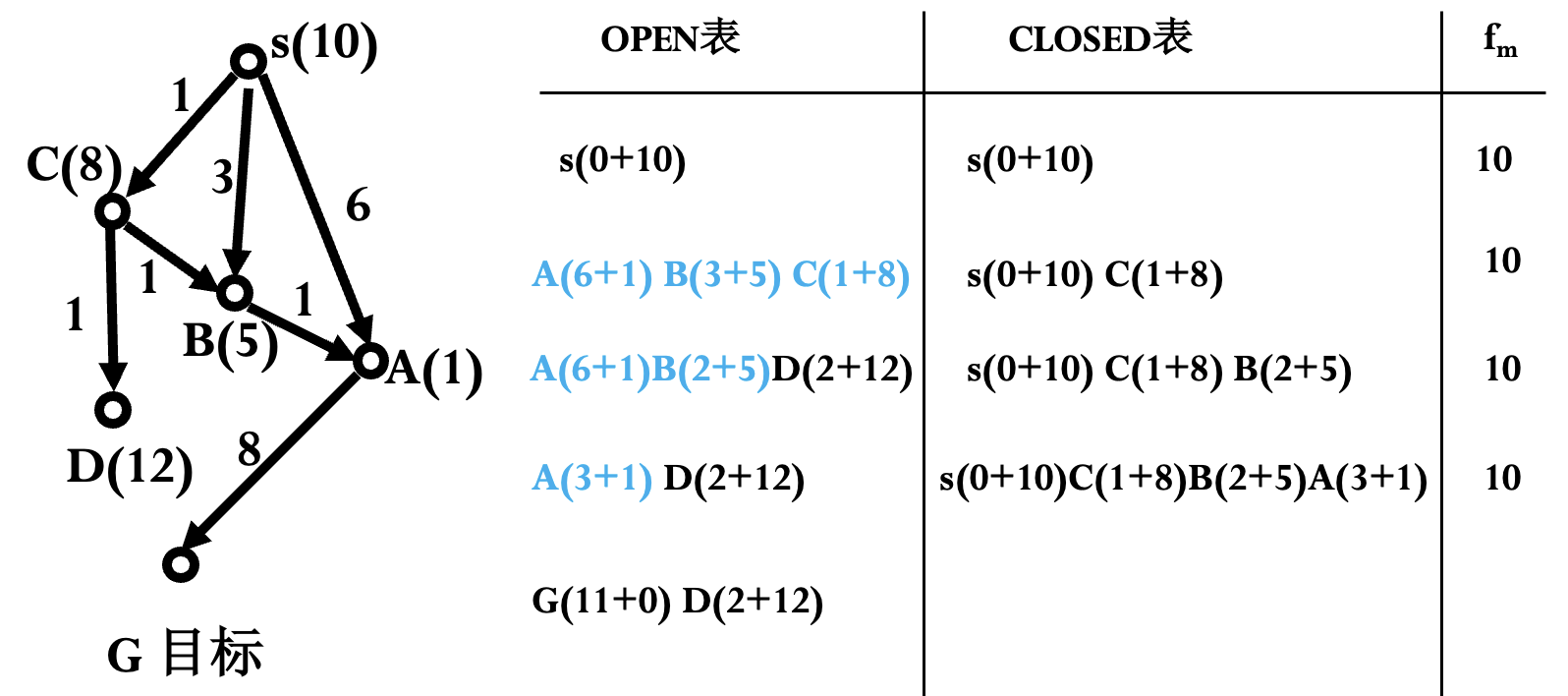
```

其他的搜索算法

局部搜索算法: 爬山法.
随机搜索算法.
动态规划算法 (当 $\forall\,n$, 有 $h(n)=0$, A* 算法即为动态规划): viterbi 算法.

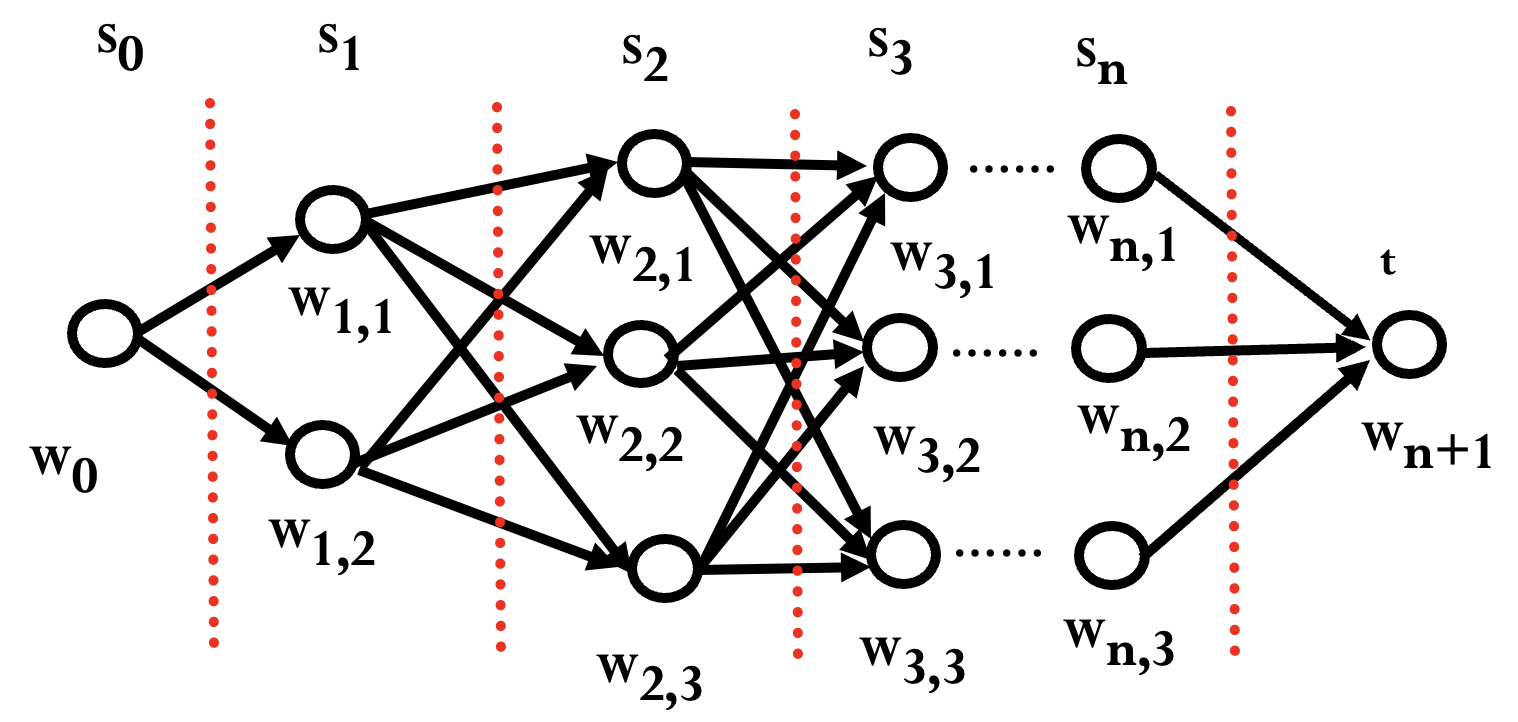
$Q(W_{i,j})=\begin{cases} \min\limits_k(Q(W_{i-1,k})+D(W_{i-1,k},W_{i,j})),&i\ne 0\\ 0,&i=0. \end{cases}$

搜索算法实用举例

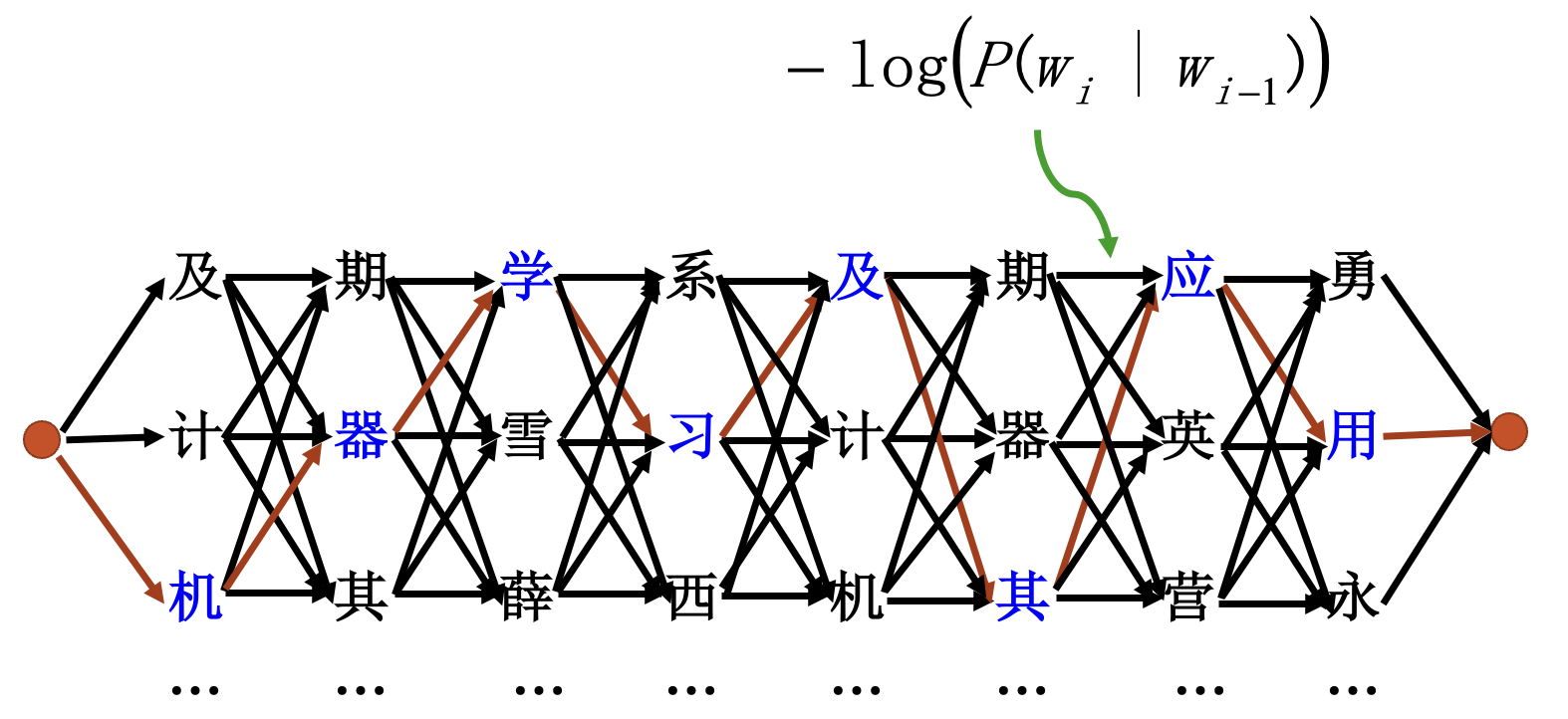
拼音输入法:
$P(S)=\prod_{i=1}^{n}P(w_i\mid w_1\cdots w_{i-1}).$
二元语法时:
$P(S)=\prod_{i=1}^{n}P(w_i\mid w_{i-1}).$
需要求
$\min\Big(-\sum_{i=1}^{n}\log\big(P(w_i\mid w_{i-1})\big)\Big)$
对应的句子.