Problem:
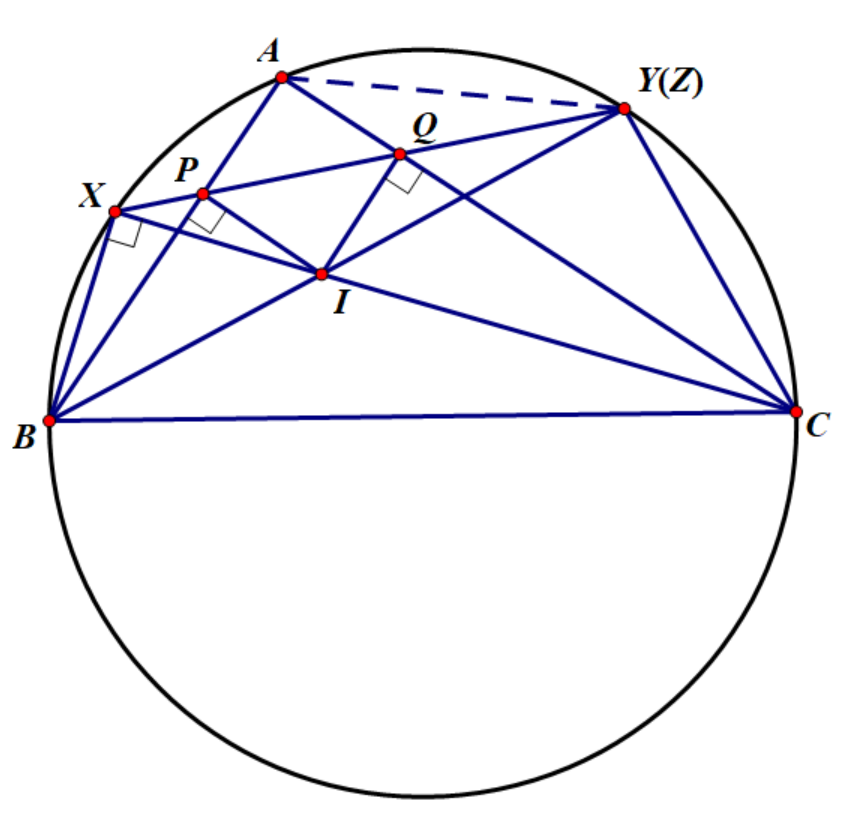
$I$是$\triangle ABC$内心, $P, Q$是$I$在$AB, AC$上的投影, 直线$PQ$交$\triangle ABC$的外接圆于$X, Y$两点, $B, I, P, X$共圆. 求证: $C, I, Q, Y$四点共圆.
Proof:
由$\angle API=\angle AQI=90^\circ$, 得$A, P, I, Q$四点共圆.
故
即$C, I, X$三点共线. 又因为$B, I, P, X$四点共圆,
知$\angle BXI=\angle BPI=90^\circ$, 即$BX\perp CX$, $BC$为$\odot ABC$的直径, $AB\perp AC$.
从而四边形$APIQ$为正方形. 取弧$\mathop{AC}\limits^{\frown}$中点$Z$, 由鸡爪定理知$ZA=ZI=ZC$成立.
从而点$Z$位于线段$AI$的垂直平分线上. 又正方形$APIQ$中, $PQ$垂直平分$AI$,
故点$Z$位于直线$PQ$上, $P, Q, Z$三点共线. 又显然点$Z$与点$X$不重合,
故点$Z$与点$Y$重合, $Y$为弧$\mathop{AC}\limits^{\frown}$中点.
由鸡爪定理知$B, I, Y$三点共线.
进而$\angle IYC=\angle BYC=90^\circ=\angle IQC$,
即$C, I, Q, Y$四点共圆.