全国高中数学联合竞赛一试模拟试题
一、填空题
1. 若点$P(x, y)$在直线$x+3y-3=0$上移动, 则函数$f(x, y)=3^x+9^y$的最小值为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $5(\frac{27}{4})^{\frac{1}{5}}$.
解析 点$P(x, y)$在直线$x+3y-3=0$上, 则有$y=\frac{3-x}{3}$, 所以
\begin{equation*}
\begin{aligned}
f(x)&=3^x+9^{\frac{3-x}{3}}=3^x+3^{2-\frac{2x}{3}} \\
&=\frac{1}{2}\cdot 3^x + \frac{1}{2}\cdot 3^x + 3^{1-\frac{2x}{3}} + 3^{1-\frac{2x}{3}} + 3^{1-\frac{2x}{3}} \\
&\ge 5\cdot\sqrt[5]{\frac{1}{2}\cdot 3^x\cdot\frac{1}{2}\cdot 3^x\cdot 3^{1-\frac{2x}{3}}\cdot 3^{1-\frac{2x}{3}}\cdot 3^{1-\frac{2x}{3}}} \\
&=5(\frac{27}{4})^{\frac{1}{5}}.
\end{aligned}
\end{equation*}
2. 已知方程$x^2+(4+i)x+4+ai=0 ($其中$a\in\mathbb{R})$有实根$b$, 且$z=a+b i$, 那么复数$z=\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $2-2i$.
解析 将$x=b$代入方程, 有$(b+2)^2+(a+b)i=0$.
分别令实部和虚部为零可得$a=2, b=-2$, 所以$z=2-2i$.
3. 若实数$x, y$满足$\tan x=x, \tan y=y$, 且$|x|\ne |y|$, 则$\frac{\sin (x+y)}{x+y}-\frac{\sin (x-y)}{x-y}$的值为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $0$.
解析 由题意, 得
同理
故
4. $\sum_{k=1}^{2022} \left[\sqrt[4]{\frac{2022}{k}}\right]$的值为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $2183$.
解析 所求的值为曲线$y=\sqrt[4]{\frac{2022}{x}}$与$x>0, y>0$所围区域内整点的数目.
将按列计数改为按行计数, 所求为
5. 在数列${\left\{a_n\right\}}$中, $a_n=\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n}+\sqrt{n+1})(\sqrt{n-1}+\sqrt{n+1})}$, 则数列$\left\{ a_n \right\}$前2022项的和为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $\frac{1}{2}(1+\sqrt{2022}-\sqrt{2023})$.
解析 \begin{equation*}
\begin{aligned}
a_n&=\frac{1}{(\sqrt{n-1}+\sqrt{n})(\sqrt{n}+\sqrt{n+1})(\sqrt{n-1}+\sqrt{n+1})} \\
&=\frac{1}{\sqrt{n-1}+\sqrt{n+1}}-\frac{1}{\sqrt{n}+\sqrt{n+1}} \\
&=\frac{\sqrt{n+1}-\sqrt{n-1}}{2}-\sqrt{n+1}+\sqrt{n} \\
&=\frac{(\sqrt{n}-\sqrt{n+1})+(\sqrt{n}-\sqrt{n-1})}{2}.
\end{aligned}
\end{equation*}
所以
\begin{equation*}
\begin{aligned}
S_{2022}&=\frac{1}{2}(1-\sqrt{2}+\sqrt{2}-\sqrt{3}+\cdots +\sqrt{2022}-\sqrt{2023})+\frac{1}{2}(1-0+\sqrt{2}-1+\cdots +\sqrt{2022}-\sqrt{2021}) \\
&=\frac{1}{2}(1-\sqrt{2023})+\frac{1}{2}\sqrt{2022} \\
&=\frac{1}{2}(1+\sqrt{2022}-\sqrt{2023}).
\end{aligned}
\end{equation*}
6. 过四面体$ABCD$的顶点$D$作半径为1的球, 该球与四面体$ABCD$的外接球切于点$D$, 且与面$ABC$相切. 若$AD=2\sqrt{3}, \angle BAD=\angle CAD=45^\circ, \angle BAC=60^\circ$, 则四面体的外接球半径$r$为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $3$.
解析 过点$D$作平面$ABC$的垂线, 垂足为$H$; 作$DE\bot AB$, 垂足为$E$; 作$DF\bot AC$, 垂足为$F$.
那么$HE\bot AB$, $HF\bot AC$, 且$AE=AF=AD\cos45^\circ =\sqrt{6}.$
由$\triangle AEH\cong\triangle AFH$, 得$\angle HAE=30^\circ$, $AH=\frac{AE}{\cos 30^\circ}=2\sqrt{2}, DH=\sqrt{AD^2-AH^2}=2,$
故$DH$为半径是$1$的球的直径,
那么四面体$ABCD$的外接球的球心$O$在$DH$的延长线上, 有
7. 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左顶点为$A$, 右焦点为$F$. 设$P$为第一象限中双曲线上的任意一点, 若总有$\angle PFA=2\angle FAP$, 则双曲线的离心率为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $2$.
解析 由题设, 可以取双曲线上的点$P$, 使$PF\bot x$轴, 得$P(c, y)$, 则$\frac{c^2}{a^2}-\frac{y^2}{b^2}=1$,
故$y^2=\frac{b^4}{a^2}$.因为$y>0$, 所以$y=\frac{b^2}{a}=\frac{c^2-a^2}{a}$.
由$\angle PFA=2\angle FAP =\frac{\pi}{2},$得$\triangle AFP$是等腰三角形, 有$AF=PF$,
即$a+c=\frac{c^2-a^2}{a}$, 整理得
又$e>1,$解得$e=2$.
8. 正整数集合$A_k$的最小元素为1, 最大元素为2022, 并且各元素可以从小到大排成一个公差为$k$的等差数列, 则并集$A_{43}\cup A_{47}$中的元素个数为$\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}.$
答案 $90$.
解析 用$|A_k|$表示集合$A_k$的元素个数.
设$|A_k|=n+1$, 由$2022=1+nk$, 得$n=\frac{2021}{k}$, 于是
故
二、解答题
9. 已知实数$x, y$都在区间$(-2, 2)$内, 且$xy=-1$, 常数$a\in (2, 8)$, 求函数$f(x, y)=\frac{4}{4-x^2}+\frac{a^2}{a^2-y^2}$的最小值.
解析 设$m=\frac{x}{2}, n=-\frac{y}{a}, m,n\in (-1, 1), mn=\frac{1}{2a}, f(x, y)=\frac{1}{1-m^2}+\frac{1}{1-n^2}$.
由柯西不等式, 得
所以
当$m=n=\frac{1}{\sqrt{2a}},$即$x=\sqrt{\frac{2}{a}}, y=-\sqrt{\frac{a}{2}}\in (-2, 2)$(注意$a\in (2, 8))$时, 不等式中的等号可成立.
所以函数$f(x, y)$的最小值为$\frac{4a}{2a-1}$.
10. 椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为$F_1$、$F_2$, 右顶点为$A$, $P$为椭圆上任意一点, 已知$\overrightarrow{PF_1} \cdot \overrightarrow{PF_2}$的最大值为3, 最小值为2.
(1)求椭圆$C$的方程.
解析 椭圆的方程为$C:\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)若直线$l:y=kx+m$与椭圆$C$相交于$M, N$两点$(M, N$不是左、右顶点$)$, 且以$MN$为直径的圆过点A, 求证: 直线$l$过顶点, 并求出该定点的坐标.
解析 设点$M(x_1, y_1), N(x_2, y_2)$.
将$y=kx+m$代入椭圆的方程, 得
所以
进而$y_1y_2=k^2x_1x_2+km(x_1+x_2)+m^2$.
因为以$MN$为直径的圆过点$A$, 所以$\overrightarrow{AM}\cdot\overrightarrow{AN}=0$, 所以
解得$m=-\frac{2}{7}k$, 或$m=-2k$, 均满足$\Delta >0$.
若$m=-2k$, 直线$l$恒过定点$(2, 0)$, 不合题意, 舍去;
若$m=-\frac{2}{7}k$, 直线$l:y=k(x-\frac{2}{7})$恒过定点$(\frac{2}{7}, 0)$.
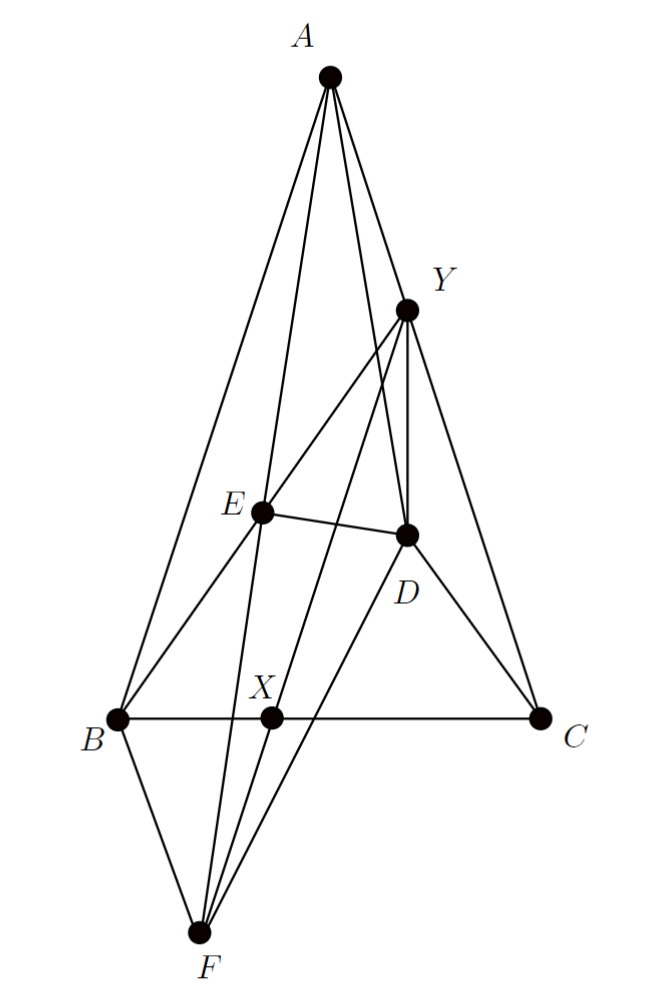
11. 在等腰$\triangle ABC$中, $AB=AC$. 设$X, Y$分别在边$BC, CA$上, 且$XY//AB$. 记$\triangle CXY$的外心为$D$, $BY$的中点为$E$. 求证:$\angle AED=90^\circ.$
解析 过$B$作$BF//AY$, 交$YX$的延长线于$F$.
由$BF//AY,AB//XY$知四边形$ABFY$为平行四边形.
由$E$为$BY$的中点,得$E$为$AF$的中点.
由$AB=AC$,有$\angle ABC = \angle ACB$,于是$\angle YXC=\angle ABC$,从而$YX=YC$.
连接$FD, DC, DA, DY$,则$\angle FYD = \angle CYD$.
由$AC=YF,DY=DC,\angle DCA=\angle DYF$,知$\triangle ADC\cong\triangle FDY$.
有$DA=DF$,而$E$为$AF$的中点,则$DE\bot AF$,即$\angle AED=90^\circ$.